12-я Международная научная олимпиада по математике для студентов университетов
10–13 июля 2007
Тегеран, Иран
I. Математический анализ (математика и прикладная математика)
1. (25 баллов) Предположим, что функция

удовлетворяет следующим двум условиям:
i)

компактно для любого компактного множества

в

;
ii)

для любой убывающей последовательности

компактных множеств в

.
Доказать, что

непрерывна.
2. (25 баллов) Предположим, что

— вещественнозначная дважды дифференцируемая функция, определенная на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
. Показать, что существуют

,

в
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
, такие, что

3. (25 баллов) Пусть

— последовательность функций со следующими свойствами:
i) каждая

(

) — периодическая функция с периодом

;
ii) каждая

(

) непрерывна на

;
iii) последовательность

равномерно ограничена на

.
Тогда

— равностепенно непрерывная последовательность функций на
![$[0,T]$ $[0,T]$](https://dxdy-03.korotkov.co.uk/f/a/a/b/aab0f08201b211261f795050337fa8df82.png)
.
Доказать или опровергнуть это утверждение.
4. (25 баллов) Предположим, что

непрерывна и

. Показать, что для каждого

 II. Численный анализ (математика и прикладная математика)
II. Численный анализ (математика и прикладная математика)
1. (25 баллов) Пусть

— функция, определенная на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
, со свойствами:
i) если
![$x\in[a,b]$ $x\in[a,b]$](https://dxdy-04.korotkov.co.uk/f/3/d/b/3db4fad11f41309c654cc9904d338f0082.png)
, то
![$g(x)\in[a,b]$ $g(x)\in[a,b]$](https://dxdy-01.korotkov.co.uk/f/c/4/4/c44dcdaacf7e8485c516495b319c7a5a82.png)
;
ii)

непрерывна на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
;
iii) для всех
![$x\in[a,b]$ $x\in[a,b]$](https://dxdy-04.korotkov.co.uk/f/3/d/b/3db4fad11f41309c654cc9904d338f0082.png)
:

.
1) Доказать, что уравнение

имеет ровно один корень на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
.
2) Показать, что если условие i) не выполнено, то уравнение

может не иметь корней на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
.
2. (25 баллов) Пусть

непрерывна на
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
,

и

,

,

.
1) Найти весовые коэффициенты в квадратурных формулах Ньютона-Котеса открытого типа:

2) Найти трехточечную квадратурную формулу Ньютона-Котеса открытого типа для

.
3) Почему квадратурные формулы Ньютона-Котеса открытого типа обычно не используются?
3. (25 баллов) Пусть

— фиксированное положительное вещественное число; определим

Предположим, что

таково, что последовательность

сходится.
1) Найти

.
2) Определить скорость сходимости последовательности

.
4. (25 баллов) Найти коэффициенты

,

,

,

,

,

и

, при которых для дифференциального уравнения

формулы Рунге-Кутта

соответствуют разложению Тейлора порядка

.
III. Алгебра (математика)
1. (25 баллов) Пусть

— кольцо с единицей.
Доказать, что:
1) Если каждый обратимый элемент централен, то каждый нильпотентный элемент централен.
2) Если каждый нильпотентный элемент централен, то каждый идемпотентный элемент централен.
2. (25 баллов) Пусть

— нециклическая группа порядка

, где

— простое число. Доказать, что у

не менее

подгрупп.
3. (25 баллов) Пусть

— конечная группа ровно с 50-тью силовскими 7-подгруппами. Пусть

и

.
1) Доказать, что

— максимальная подгруппа

.
2) Если у

есть силовская 5-подгруппа

и

, то доказать, что

.
4. (25 баллов) Пусть

— такое кольцо, что из

следует, что

. Пусть для всех

:

. Доказать, что

коммутативно.
Исследование операций (прикладная математика)
1. (25 баллов) Матрица

размера

,

, с целыми элементами называется вполне унимодулярной, если каждая подматрица

, составленная из набора

различных столбцов

, такова, что

(любая такая

также называется унимодулярной).
1) Доказать, что если целочисленная матрица

размера

унимодулярна, то

также унимодулярна (и целочисленна).
2) Рассмотрим задачу линейного программирования:

где

— целочисленная матрица размера

,

, и

— целочисленный вектор. Доказать, что если

вполне унимодулярна и у (LP) есть оптимальное решение, то симплекс-метод для задачи (LP) найдет оптимальное целочисленное решение (в предположении, что (LP) невырожденна).
2. (25 баллов) Рассмотрим задачу линейного программирования:

где

и

заданы. Доказать, что:
1)

— оптимальное решение (LP) тогда и только тогда, когда выполнено:
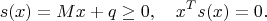
2) Две допустимые точки

и

для (LP) являются ее оптимальными точками тогда и только тогда, когда выполнено:

3) Если

, то у задачи (LP) есть оптимальное решение.
3. (25 баллов) Доказать 1) и 2), используя элементарные определения выпуклых множеств и выпуклых функций.
1) Показать, что множество

выпукло.
2) Показать, что если

— оптимальное (локальное) решение задачи

то

— глобальное решение.
Доказать или опровергнуть 3) и 4).
3) Задача (LP) может быть недопустимой.
4) Задача (LP) может быть неограниченной.
4. (25 баллов) Предположим, что

— непустое открытое выпуклое множество в

и

дифференцируема на

. Доказать, что если

выпукла на

, то выполнено:
 IV. Линейная алгебра (математика и прикладная математика)
IV. Линейная алгебра (математика и прикладная математика)
1. (33.3 балла) Пусть

и
![$\mathbb{C}[A]=\{f(A)\mid f(x)\in\mathbb{C}[x]\}$ $\mathbb{C}[A]=\{f(A)\mid f(x)\in\mathbb{C}[x]\}$](https://dxdy-01.korotkov.co.uk/f/4/4/b/44b6342e8950c59a5bdebabf1cf1282082.png)
. Доказать, что у кольца
![$\mathbb{C}[A]$ $\mathbb{C}[A]$](https://dxdy-02.korotkov.co.uk/f/1/6/a/16a0e55857da5113367b8b9cda67004a82.png)
нет ненулевых нильпотентных элементов тогда и только тогда, когда

диагонализируема.
2. (33.3 балла) Доказать, что если

— натуральное число, то существует такая обратимая матрица

размера

, что

,

и

для всех

.
3. (33.3 балла) Пусть

— обратимая матрица со столбцами

. Пусть

— матрица со столбцами

. Показать, что у матриц

и

ранг

, а их собственные числа — только нули.
Оригиналы условий на английском:
http://www.mathlinks.ro/Forum/viewtopic.php?t=158736
Результаты:
http://olympiad.sanjesh.org/EnglishV/Ne ... 31124.aspx



