Вобщем,задача такова:
Плотность вероятности СНСВ
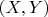
имеет вид


плотность такая же,как в конце поста в [] . Здесь почем-то неправильно отображает
Найти
1)

2)безусловные плотности вероятности

и

3) определить,зависимы ли

и

Помогите пожалуйста. Знаю,что можно решить таким образом
![$P = \int\limits_{ - 0.5}^{0.5} {dx} \int\limits_{ - 1}^1 {dy} \left[ {\frac{1}{{2\pi }}\mathop e\nolimits^{ - \frac{{\mathop x\nolimits^2 + \mathop y\nolimits^2 }}{2}} } \right]$ $P = \int\limits_{ - 0.5}^{0.5} {dx} \int\limits_{ - 1}^1 {dy} \left[ {\frac{1}{{2\pi }}\mathop e\nolimits^{ - \frac{{\mathop x\nolimits^2 + \mathop y\nolimits^2 }}{2}} } \right]$](https://dxdy-04.korotkov.co.uk/f/3/0/9/309684d889446918183fab1e348293e782.png)
но смущает что-то,т.к. обычно в задаче плотность имеет вид попроще. Может можно её как-то упростить?