Здравствуйте
Я в первый раз пишу на этот форум, такчто извините если что-нибудь не так.
Читаю "Quantum Mechanics: A Modern Development" by Lesli E Ballentine ([url=http://books.google.co.uk/books?id=sHJRFHz1rYsC&pg=PA613&lpg=PA613&dq=irreducible+set+of+operators&source=bl&ots=RoG-PcdhW0&sig=aHEPIclmXdPdQTMBSVpaUe_uSgg&hl=en&sa=X&ei=3n-cUen9CIKW0AWXs4CICQ&ved=0CC4Q6AEwAA#v=onepage&q=irreducible%20set%20of%20operators&f=false]
можно посмотреть здесь[/url]). В третьей главе он выводит правила кинемтики для кванотвых частиц.
Вначале выводятся коммутаторы между десятью генераторами транформаций группы Галилея.

- генератор смещений в пространстве

- генератор изменения скорости

- генератор вращений

- генератор трансляции во времени
![$[P_\alpha,P_\beta]=0, \quad
[G_\alpha,G_\beta]=0, \quad
[J_\alpha, \{J_\beta,G_\beta,P_\beta\}]=i\varepsilon_{\alpha\beta\gamma}\{J_\gamma,G_\gamma,P_\gamma\}, \quad
[H,\{J_\alpha,P_\alpha\}]=0, \quad
[G_\alpha,H]=iP_\alpha, \quad
[G_\alpha,P_\beta]=i\delta_{\alpha,\beta}MI
$ $[P_\alpha,P_\beta]=0, \quad
[G_\alpha,G_\beta]=0, \quad
[J_\alpha, \{J_\beta,G_\beta,P_\beta\}]=i\varepsilon_{\alpha\beta\gamma}\{J_\gamma,G_\gamma,P_\gamma\}, \quad
[H,\{J_\alpha,P_\alpha\}]=0, \quad
[G_\alpha,H]=iP_\alpha, \quad
[G_\alpha,P_\beta]=i\delta_{\alpha,\beta}MI
$](https://dxdy-04.korotkov.co.uk/f/3/b/2/3b2a42d2b9c7de4744f76bf56dd974a182.png)
Где

-это константа а

- это единичный оператор
NB!
Хоть символы выбранные для генераторов и подобраны чтобы совпадать с общепринятой нотацией, на этой стадии это просто генераторы (тоесть
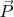
- не импульс а

- не Гамильтониан).
После этого вводится оператор позиции частицы (

) и получаются коммутаторы этого оператора с десятю генераторами. Коммутатор с

получается из


![$V_\alpha=i[H,Q_\alpha]$ $V_\alpha=i[H,Q_\alpha]$](https://dxdy-01.korotkov.co.uk/f/8/2/3/823919d079385fb680b8c96ce2ffcaee82.png)
. Где

это оператор скорости.
Во всех остальных коммутаторах

ведёт себя как

. Этого конечно не достаточно чтобы приравнять эти два оператора, но автор подмечает что оператор

коммутирует и с

и с
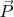
(и с

).
Теперь автор переходит к рассмотрению кинематики свободной частицы без полей и без 'internal degrees of freedom' (не знаю верный перевод). И на основе этого делает вывод что

образуют 'irreducible set', так что если какой-либо оператор коммутирует с этими двумя членами set'а то этот оператор равен единичному оператору помноженному на произвольную константу (Schur's Lemma).
ВОТ ЭТО ШАГ мне и не ясен. Почему 'irreducible set'? Почему именно эти операторы?
Большое спасибо за помощь.
PS: После этого автор может сделать вывод что

, ну а там уже понятно.
PPS:Сам подход (по признанию автора) основан на статье T. F. Jordan, "Why is

the momentum", Am. J. Phys. 43, p 1089 (1975). Статью посмотрел, но это мало помогло.



