Пусть выпуклый четырёхугольник называется
нестандартным, если в нём существует такая точка

, что сумма расстояний от неё до вершин больше периметра этого четырёхугольника.
Существует ли нестандартный четырёхугольник?
У меня решение было немного арифметическое:
Пусть наш четырёхугольник образован точками

Тогда сумма расстояний от точки

до вершин равна

А периметр равен

В официальном решении пример
немного иной. У них там
 Интересно было бы дальше порассуждать.
Интересно было бы дальше порассуждать.Какие вообще бывают нестандартные четырёхугольники? Существует ли предел отношения суммы расстояний от точки

до вершин к периметру? Мне кажется, что этот предел равен
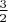
. Во всяком случае, если обобщить мой пример и построить четырёхугольник

и взять в нём точку

, то сумма расстояний будет больше

, а периметр будет меньше

.