Вид функции смущает. Все-таки степень

должна быть внутри синуса, чтобы было бесконечное число колебаний. А если

, не будет непрерывности в 0.
Вот простое рассуждение. Пусть на отрезке
![$[a;b]$ $[a;b]$](https://dxdy-04.korotkov.co.uk/f/f/5/f/f5ff45e36cee967b17a810445d436aaa82.png)
производная по модулю не превосходит

. Разобьем его на части длиной

, вариация на каждом по модулю не превосходит

, а сумма квадратов не больше

. Как вы видите, при условии ограниченности производной квадратичную вариацию можно устремить к 0. Правда, это еще не означает, что такое стремление будет обязательно.
-- 21.05.2013, 22:01 --Подумала еще. В предыдущем утверждении использовалось то, что все отрезки разбиения равны,тогда их не более

, но вообще-то некоторые отрезки могут быть короче, тогда их будет больше. Но это можно обойти.
Квадратичная вариация не превосходит

. Пусть длина каждого отрезка меньше

. Будем добавлять к первому отрезку следующие, пока сумма длин не станет больше

(но меньше, конечно,
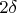
). Сумма квадратов длин в такой группе будет самой большой, если все они представляют собой один отрезок.
Итак, сумма квадратов длин не превосходит

. Значит, эта сумма стремится к 0 при
