Надо же, оказывается, мне уже три года стыдно за этот должок. Пообещал и не сделал.
Но меня просят (через ЛС) развить тему, рассказать, что я знаю про эту задачу.
И я постараюсь довести это до ума.
Литературы в своём бумажном архиве я не нашёл. По жизни следил я за журналами
CAD,
CAGD,
JCAM. Теперь журналов развелось много; и я уже почти не слежу. Гуглить можно "circular spline", "arc spline (approximation)".
Задачу, которую я намерен осветить, можно сформулировать так:
Найти кривую с кусочно-постоянной кривизной, аппроксимирующую заданную кривую  с заданной точностью.
с заданной точностью.Предлагаемое решение идёт чисто из моей головы; других (решений) не знаю. Результирующая кривая с кусочно-постоянной кривизной состоит, понятно, из гладко сопряжённых кусочков прямых и окружностей.
Так что речь идёт не только о сплайнах:

--- произвольная достаточно приличная кривая, о которой мы знаем или можем узнать всё. Из этого всего понадобятся наклон касательной

, кривизна

и решения уравнения

, т.е. экстремумы кривизны (вершины кривой). Функция
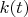 не обязана
не обязана быть непрерывной.
Мы разбиваем кривую на достаточно малые отрезки-дуги следующим образом:
(1) выделяем вершины кривой; таким образом, кривизна на каждом участке будет монотонна, что впоследствии и позволит сгаранатировать точность аппроксимации;
(2) разбиение кривой внутри каждого участка должно быть как минимум таким, чтобы каждая дуга однозначно проектировалась на свою хорду (будет там внутри перегиб или нет --- нам до лампочки); уже на этом этапе мы сможем определить точность будущей аппроксимации и, если она недостаточна, вставить промежуточную точку.
Пункт (2) можно реализовать в виде сканированя кривой с неким мелким шагом

, с выбором очередного узла

будущего circular spline исходя из наперёд заданной точности

. Замечу, что нам не нужны точки перегиба кривой и узлы оригинального сплайна.
Нижеприведённая картинка нарисована по несколько иному поводу, и не является иллюстрацией предлагаемого алгоритма (он даст несколько б
ольшую точность). Но кое-что она проясняет и иллюстрирует.

а) Заданная кривая, представленная мелкими точечками, --- спираль Корню. У неё, как известно, нет вершин: кривизна --- линейная функция длины дуги. Поэтому первый этап разбиения отменяется, и мы начали со второго. Выбрали 11 точек, соблюдя условие однозначного проектирования на хорду.
b) Серенькие области --- некие оценки точности интерполяции/аппроксимации (повторяю --- это некий другой алгоритм). Здесь важно то, что монотонность кривизны не позволяет никакой аппроксимирующей кривой (тоже с возрастающей или тоже с убывающей кривизной, с некими граничными условиями на закреплённых концах) выйти за эти пределы.
c) Количество узлов увеличено с 11 до 15. При увеличении количества точек в n раз ширина области уменьшается в n^3 раз.
Писать буду по частям: так мне психически проще. Это была интродукция; вопрошавшие пусть видят, что я начал отвечать.
update: 05.01.2011 - переместил рисунок