Вопрос актуальный. Как я писал в теме "x-1/x", вычисление рекуррентных последовательностей, особенно таких как

, очень чувствительно к погрешностям. И влияние на характерные особенности поведения последовательности начинает оказываться довольно быстро.
Как производится, например, сложение

? При таком кол-ве значащих разрядов должно произойти, видимо вот что: второе слагаемое округляется до

и результат получается

. Значит,
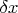
второго слагаемого не

, а аж

, и всё, вычисления испорчены. За 100 итераций погрешность достигает 100%.
И это не считая странной фишки форматов семейства
float, когда несколько младших разрядов (1-3) отличаются изначально от заданного значения. Например, если написать
float a=4.0 , то проверка может показать, что a равно чему то типа
4.000000000035 . И как с этим работать?
Во первых, надо понимать, что такое float и double, с чем их едят, и почему последние цифры не хотят обнуляться. В идеале прочитать
http://docs.oracle.com/cd/E19957-01/806 ... dberg.html .После этого Вы уже сможете понять, хватит ли Вам возможностей процессорной floating-point арифметики.
Во-вторых, есть библиотеки для вычислений с высокой точностью, напр.
MPFR.
В-третьих, такие штуки можно считать в виде точных рациональных чисел

. Только знаменатели часто растут экспоненциально, поэтому все равно потребуется либо библиотека целых чисел типа
GMP или
MPIR или язык программирования, в котором встроен тип длинных чисел с помощью такой библиотеки, напр. Haskell, Python или что-нибудь специализированное математическое.



