Это какая по определенности матрица?

[A'Y]

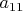
Если у симметричной матрицы $A$ размерности $2\times2$ первый главный минор (элемент $a_{11}$) положительный, а второй главный минор ($a_{11}a_{22}-a_{12}^2$) отрицательный - то какой определенности это соответствует? Ясно, что не положительно определена, и что не отрицательно. А вот другие способы определенности (положительная полуопределенность, отрицательная полуопределенность) я не знаю как зависят от знаков главных миноров.

[provincialka]

"Никак не определена" . Неопределенная.
Посмотрите в литературе, какой определитель (второй минор) должен быть у полуопределенной матрицы.

[A'Y]

А если $a_{11}$ иногда принимает положительные, а иногда - отрицательные значения. Тоже никак не определена?

[provincialka]

Никак не определена - это я пошутила, кавычки там. Просто есть непределенные матрицы (соотвествующие им квадратичные формы принимают и положительные, и отрицательные значения).

Слово "иногда" непонятно. У вас матрица переменная, что ли? Свойство определенности/неопределенности относится к фиксированной матрице, если матрица переменная, ее характеристика тоже может меняться.

[A'Y]

Элементы матрицы зависят от одного параметра. Второй главный минор ($a_{11}a_{22}-a_{12}^2$) всегда отрицательный; так что хоть параметр и меняется, на определённость это не влияет. А вот первый главный минор ($a_{11}$) в зависимости от параметра может быть или положительным, или отрицательным.

[provincialka]

Несостыковка. В исходном сообщении второй минор отрицателен! В этом случае знак первого минора не важен.

Кстати, у вас минор записан неверно. Там квадрат, а не удвоение.

[A'Y]

provincialka в сообщении #714203 писал(а):

В исходном сообщении второй минор отрицателен!

Оговорился.

provincialka в сообщении #714203 писал(а):

В этом случае знак первого минора не важен.

Почему?

provincialka в сообщении #714203 писал(а):

Там квадрат, а не удвоение.

Описался.

[provincialka]

Легче всего понять через соотв. квадратичную форму. Если она положительно определена, то по всем направлаениям ее значения положительны. Вчастности, и для $y=0$. Аналогичная картина для отрицательной определенности.

Если же форма неопределенная, по некоторым направлениям значения положительны, по другим - отрицательны. Так что и вдоль оcи $Ox$ знак может быть любым.

[A'Y]

Есть теорема (в линейной алгебре вроде обычно даётся) о том, что по сочетанию знаков ведущих миноров матрицы из вторых производных квадратичной формы можно установить соответствующий характер поведения функции в малой окрестности: локальный минимум / локальный максимум / седловая точка / неизвестно.

Подскажите, где можно найти эту теорему в учебниках (желательно классических)? Надо сослаться на неё в курсовике.

Две ветки на одну тему слиты. / GAA, 30.04.2013

[SpBTimes]

Любой приличный учебник по анализу.

[A'Y]

Например? Просмотрел Зорича, не нашёл.

-- 30.04.2013, 10:38 --

Если вдруг кто может конкретно ткнуть, был бы рад.
У меня кроме Зорича ещё Шварц есть, но я его ниасилю просмотреть.

[SpBTimes]

Зорич, том 1, глава 8, параграф 4, теорема 6 и далее.

[bot]

SpBTimes в сообщении #717564 писал(а):

Любой приличный учебник по анализу.

Критерий Сильвестра излагают обычно в учебниках по алгебре.