Здравствуйте,
На днях встретил задачу:
"Найти все возможные уравнения, используя числа

единожды каждое, операторы

- любое количество раз для построения левой его части и число 381 - для построения правой части соответственно."
Логика поиска:
1) 4 позиции для операторов, 4 претендента:

,
2) 5 позиций для чисел, 5 претендентов, выбран должен быть каждый:
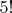
,
3) общее число возможных левых частей (комбинаторно, т. е. включая те, которые не равны 381):

,
4) указанное число левых частей было сгенерировано и проверено на равенство 381, ни одна из проверяемых таковой не оказалась.
Тем не менее, в источнике указано, что такие уравнения существуют, и что с этим заданием должен справиться даже ребенок в достаточно короткое время.
Возможно я упускаю что-то очевидное, прошу помочь разобраться и внести объективность в данную ситуацию, за что заранее благодарен.