 Kyiv Taras Shevchenko University Mechmat Competition
Kyiv Taras Shevchenko University Mechmat Competition
6 March 2013Problems for 1st and 2nd year students1. Find all such continuous functions
![$f:[1,2]\to[1,2]$ $f:[1,2]\to[1,2]$](https://dxdy-01.korotkov.co.uk/f/c/6/2/c626c1c6a7a8a5dc75fa7fdcd59193b482.png)
that
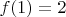
and
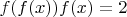
for all
![$x\in[1,2]$ $x\in[1,2]$](https://dxdy-02.korotkov.co.uk/f/9/7/7/97793f083fd8ce2771677d51994ec1e682.png)
. (Ivan Feshchenko)
2. Does there exist such a finite ring (not necessarily commutative or with a unit) that for every its element

there exists such an element

different from

that
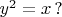
(Sergiy Slobodianiuk)
3. In a given triangle the lengths of sides and tangents of angles are arithmetic progressions. Find the angles. (Alexander Kukush, Maria Rozhkova)
4. Let
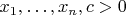
. Prove the inequality
![$$\[\sqrt{{x_1+\sqrt{{x_2+\sqrt{{\ldots+\sqrt{x_n+c}}}}}}}<\sqrt{{x_1+\sqrt{{x_2+\sqrt{{\ldots+\sqrt{x_n}}}}}}}+\dfrac{c}{2^n\,\sqrt{{x_1\ldots x_n}}}\,\,.\]$$ $$\[\sqrt{{x_1+\sqrt{{x_2+\sqrt{{\ldots+\sqrt{x_n+c}}}}}}}<\sqrt{{x_1+\sqrt{{x_2+\sqrt{{\ldots+\sqrt{x_n}}}}}}}+\dfrac{c}{2^n\,\sqrt{{x_1\ldots x_n}}}\,\,.\]$$](https://dxdy-02.korotkov.co.uk/f/d/8/8/d88b3b992ccc7be445be6df2b2f1dcc982.png)
(Ivan Feshchenko)
5. Let

be such

matrices that for every

matrix

the equation
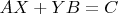
has a solution

. Prove that then for every matrix

the equation
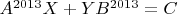
has a solution too. (Ivan Feshchenko)
6. There are given such functions
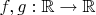
that for every two different numbers

either the inequality
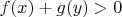
or inequality
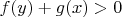
holds. Prove that there do not exist such numbers

and

that for all
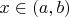
the inequality
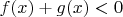
holds. (Oleksiy Rudenko)
7. A
positive integer is called good if it is the

-th power of an integer for some
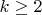
. Is finite or infinite the set of all integers that are not sums of two good integers? (Andriy Bondarenko)
8. Let

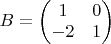
. Can a product
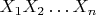
equal the unit matrix if every multiplier

equals either

or
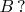
(Yevgen Makedonsky)
Problems for 3rd-5th year students1. Calculate the sum of series
![$$\[\sum_{n=0}^{\infty}\frac{1}{n!\,2^n}\cos\frac{\pi n-1}{2}.\]$$ $$\[\sum_{n=0}^{\infty}\frac{1}{n!\,2^n}\cos\frac{\pi n-1}{2}.\]$$](https://dxdy-02.korotkov.co.uk/f/d/f/6/df621bb4ed9ebe2406c16809326acfc582.png)
(Dmytro Mitin)
2. Does there exist such a finite nonzero ring (not necessarily commutative or with a unit) that for every nonzero element

there exists such an element

different from

that
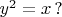
(Sergiy Slobodianiuk)
3. There are given such functions
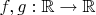
that for every two different numbers

either the inequality
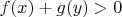
or inequality
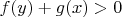
holds. Prove that there do not exist such numbers

and

that for all
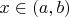
the inequality
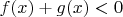
holds. (Oleksiy Rudenko)
4. Let

be such

complex matrices that for every

matrix

the equation
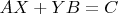
has a solution

. Prove that
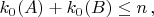
where
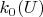
is the number of zeroes in the main diagonal of Jordan form of

. (Ivan Feshchenko)
5. Let
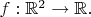
Is it always true that
![$$\[\text{ess\,sup}_{x\in\mathbb{R}}\bigl(\text{ess\,sup}_{y\in\mathbb{R}}f(x,y)\bigr)=\text{ess\,sup}_{y\in\mathbb{R}}\bigl(\text{ess\,sup}_{x\in\mathbb{R}}f(x,y)\bigr)\,?\]$$ $$\[\text{ess\,sup}_{x\in\mathbb{R}}\bigl(\text{ess\,sup}_{y\in\mathbb{R}}f(x,y)\bigr)=\text{ess\,sup}_{y\in\mathbb{R}}\bigl(\text{ess\,sup}_{x\in\mathbb{R}}f(x,y)\bigr)\,?\]$$](https://dxdy-04.korotkov.co.uk/f/f/3/c/f3c10aa7fb3efd0ffdbdf66e9bec408182.png)
(Here the essential supremums are taken with respect to Lebesgue measure on the line). (Alexander Kukush)
6. Do there exist such real nonconstant rational functions

and

that
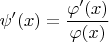
for all

from the intersection of definition domains for left and right hand sides of the equality? (Yevgen Makedonsky)
7. Let
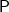
be such a probabilistic measure on Borel

-algebra on

that for every straight line

it is true that
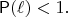
Does there always exist such a bounded Borel set

that for every straight line

it is true that
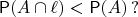
(Alexander Kukush)
8. Let

be such a sequence of real numbers that

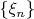
be a sequence of independent identically distributed random variables with distribution
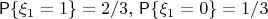
and
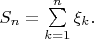
Prove that the series
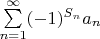
converges
in probability. (Georgiy Shevchenko)
Time allowed: 3 hours


