Определитель - это объем параллелепипеда, натянутый на векторы, из которых состоит соответствующая матрица.
К примеру, если координаты векторов

,

и
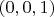
- то это куб объема 1. Соответствующая матрица будет иметь вид

определитель которой равен 1.
Можно ли построить такой параллелепипед в 3-хмерном пространстве, образующие векторы которого имеют координаты, состоящие из 0 и 1, у которого будет объем бОльше, чем у приведенного мною примера с кубом? Вообще-то да, к примеру, с векторами

,

и

получится параллелепипед, у которого объем будет больше. А существует ли еще больше?