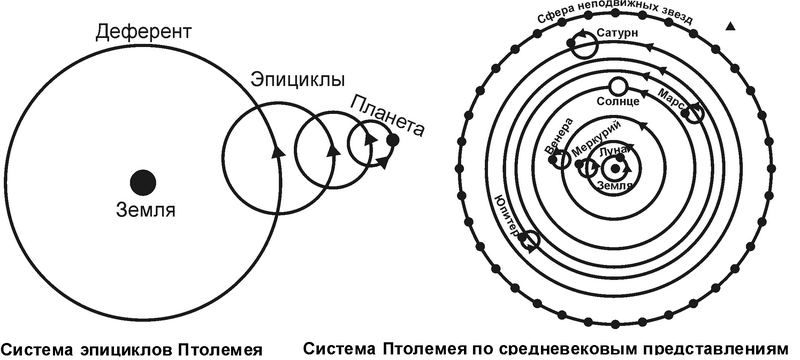
"Система эпициклов Птолемея
Вдоль деферента движется центр первого эпицикла, вдоль первого эпицикла — центр второго эпицикла, вдоль второго эпицикла — центр третьего эпицикла и т. д., наконец, вдоль последнего эпицикла движется сама планета"
[img]
[/img]
У Птолемея была задача описать ограниченную реальную конкретную действительность.
Для современных людей очень приблизительный, общий принцип движения космических тел, конечно известен.
Цепочка …, Галактика, Солнце, Земля, Луна, искусственные спутники Луны очень наглядна, но ограниченна своими законами. (Там, конечно, есть свои сложности.)
А у меня задача максимально выйти изо всех известных (другим, и думаю мне) рамок построения неограниченных комбинаций абстрактных окружностей без массы, гравитации и других сил воздействия.
На движение космических тел влияют конкретные жесткие условия, законы природы, за рамки которых выйти они не могут.
А я, думаю, учел все возможные абстрактные варианты построения комбинаций окружностей на плоскости. И максимально использовал все переменные в формуле построения цепочки окружностей.
Это позволяет создавать максимально гибко бесконечные, всевозможные графические формы на плоскости.
Деферент, эпициклы Птолемей использовал, чтобы описать движение космических тел относительно Земли в центре Вселенной. Он, наверняка, не думал о другом применении их.
И я не встречал нигде описания применения таким образом связанных окружностей для получения такого результата, как у меня.
Вот программа-формула моего применения окружностей.
Я не математик, но, думаю, что больше добавить нечего.
Настоящий математик, уверен, поймет, что здесь заключено.
Код:
X0 - координата X главной опорной центральной точки первой окружности
Y0 - координата Y главной опорной центральной точки первой окружности
X1-X6 - координата X окружностей 1 - 6 с центрами в точках X0 - X5
Xn - координата X окружностей n с центрами в точках Xn-1
Y1-Y6 - координата Y окружностей 1 - 6 с центрами в точках Y0 - Y5
Yn - координата Y окружностей n с центрами в точках Yn-1
R1-R6-Rn - величина радиусов окружностей в пикселах
F1-F6-Fn - начальное угловое отклонение радиусов
N1-N6-Nn - количество оборотов радиусов за цикл
K - коэффициент частоты расчета следующей координаты
G - угловой поворот всего рисунка
For i = 0 To (2 * K) – Next I - это организация циклического построения сдвигов отрезков графика
For i = 0 To (2 * K)
X1 = X0 + R1 * Cos((i + F1) * Pi / K * N1 + G)
Y1 = Y0 + R1 * Sin((i + F1) * Pi / K * N1 + G)
X2 = X1 + R2 * Cos((i + F2) * Pi / K * N2 + G)
Y2 = Y1 + R2 * Sin((i + F2) * Pi / K * N2 + G)
X3 = X2 + R3 * Cos((i + F3) * Pi / K * N3 + G)
Y3 = Y2 + R3 * Sin((i + F3) * Pi / K * N3 + G)
X4 = X3 + R4 * Cos((i + F4) * Pi / K * N4 + G)
Y4 = Y3 + R4 * Sin((i + F4) * Pi / K * N4 + G)
X5 = X4 + R5 * Cos((i + F5) * Pi / K * N5 + G)
Y5 = Y4 + R5 * Sin((i + F5) * Pi / K * N5 + G)
X6 = X5 + R6 * Cos((i + F6) * Pi / K * N6 + G)
Y6 = Y5 + R6 * Sin((i + F6) * Pi / K * N6 + G)
…
Xn = Xn-1 + Rn * Cos((i + Fn) * Pi / K * Nn + G)
Yn = Yn-1 + Rn * Sin((i + Fn) * Pi / K * Nn + G)
Next i