Системный анализ и исследование операций

[Riddick]

Здравствуйте! Помогите пожалуйста в составлении модели для вот такой задачи:
Распределенная информационная система включает n баз данных (БД). Стоимость обращения к БД равна С_j. Одна и та же информация может содержаться в нескольких БД. За одно обращение из БД извлекается вся необходимая информация.
Требуется найти оптимальный вариант выполнения заявки на m единиц информации для критерия "Средняя стоимость задействованной БД".
Картинку таблички с исходными данными можно посмотреть здесь

Как пытался решать Я:
Введем булеву переменную &X_i& – факт обращения к БД. Если обращение к БД было, то переменная становится равной 1, иначе 0. Таким образом:
$X_1$ – факт наличия обращения к БД1
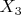
$X_2$ – факт наличия обращения к БД2
$X_3$ – факт наличия обращения к БД3
$X_4$ – факт наличия обращения к БД4
$X_5$ – факт наличия обращения к БД5
$X_6$ – факт наличия обращения к БД6
$X_8$ – факт наличия обращения к БД8
$X_9$ – факт наличия обращения к БД9
$X_1_0$ – факт наличия обращения к БД10

Средняя стоимость задействованных БД – сумма всех затрат, деленная на количество обращений ко всем БД. Таким образом, критерий можно найти так:
$ L=\frac {C_1\cdot x_1 + C_2\cdot x_2 + C_3\cdot x_3 + C_4\cdot x_4 + C_5\cdot x_5 + C_6\cdot x_6 + C_8\cdot x_8 + C_9\cdot x_9 + C_1_0\cdot x_1_0 } {x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_8 + x_9 + x_1_0 } $
А ограничения будут такими:
$ \left\{ \begin{array}{l} x_2 + x_5 =1, \\ x_1 + x_4 + x_5 =1, \\ x_2 + x_3 + x_9 =1, \\ x_2 + x_6 =1, \\ x_4 + x_5 =1, \\ x_1 + x_3 +x_5 + x_8 =1, \\ x_1 =1, \\ x_8 + x_9 =1, \\ x_4 + x_1_0 =1, \\ \end{array} \right. $

Поскольку критерий нелинейный и, соответственно, методами линейного программирования его решить нельзя, обозначим:
$ p= \frac {1} {x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_8 + x_9 + x_1_0 } $

$ \left\{ \begin{array}{l} x_2\cdot p + x_5\cdot p = p, \\ x_1\cdot p + x_4\cdot p + x_5\cdot p =p, \\ x_2\cdot p + x_3\cdot p + x_9\cdot p =p, \\ x_2\cdot p + x_6\cdot p =p, \\ x_4\cdot p + x_5\cdot p =p, \\ x_1\cdot p + x_3\cdot p +x_5\cdot p + x_8\cdot p =p, \\ x_1\cdot p = p, \\ x_8\cdot p + x_9\cdot p =p, \\ x_4\cdot p + x_1_0\cdot p =p \end{array} \right. $

Введем еще одно обозначение:
$ y_i = x_i\cdot p $

Получим:

$ \left\{ \begin{array}{l} y_2 + y_5 - p =0, \\ y_1 + y_4 + y_5 - p =0, \\ y_2 + y_3 + y_9 - p =0, \\ y_2 + y_6 - p =0, \\ y_4 + y_5 - p =0, \\ y_1 + y_3 +y_5 + y_8 - p =0, \\ y_1 - p =0, \\ y_8 + y_9 - p=0, \\ y_4 + y_1_0 - p=0, \\ y_1+y_2+y_3+y_4+y_5+y_6+y_8+y_9+y_1_0 = 1 \end{array} \right. L=C_1\cdot y_1 + C_2\cdot y_2 + C_3\cdot y_3 + C_4\cdot y_4 + C_5\cdot y_5 + C_6\cdot y_6 + C_8\cdot y_8 + C_9\cdot y_9 + C_1_0\cdot y_1_0 $

Всё! Математическая модель составлена. Теперь я пытаюсь решить эту систему пакетом LINDO. Вот код программы:

min 3y1 + 10y2 + 5y3 + 17y4 + 15y5 + 7y6 + 4y8 + 8y9 + 9y10
st
y2 + y5 -p =0
y1 + y4 + y5 -p =0
y2 + y3 + y9 -p =0
y2 + y6 -p =0
y4 + y5 -p =0
y1 + y3 + y5 + y8 -p =0
y1 -p =0
y8 + y9 -p =0
y4 + y10 -p =0
y1 + y2 + y3 + y4 + y5 + y6 + y8 + y9 + y10 = 1
end

LINDO выдаёт сообщение об ошибке №54 - решения нет, нехватка ресурса (переменная $y_3$ отрицательная).
Я, конечно, понимаю, что отсутствие решения - тоже решение, но всё-таки может быть всё дело в модели, которую Я составил. Может быть так нельзя было решать эту задачу.... Пожалуйста подскажите