Читаю учебник по мат анализу от Киркинского, и тут в доказательстве свойства пределов ( а именно что предел отношения двух последовательностей равен отношению пределов этих последовательностей, учитывая что последовательность стоящая в знаменателе напр

и ее предел
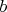
не равны нолю). Пропущу первую часть рассуждения - она мне понятна до места где автор говорит, что т.к.

, то

[в последнем сравнении

стоит в модуле, как не бился он не ставился в конструкторе формул]. Собственно вопрос : справедлив ли вывод который сделал автор только из того что

не бесконечно убывающая последовательность а

ее предел? В голову пришел такой пример

, так пределом такой последовательности будет являться единица, но не существует такого

начиная с которого все члены последовательности будут меньше

т.к. последовательность убывает от 3 до 1. Помогите разрешить эту дилемму. Если автором был сделан закономерный вывод, пожалуйста объясните почему это так. Заранее большое спасибо за все ответы.