Подскажите, где прочитать про построение полиномов (конечной степени) наилучшего приближения в
![$C[a,b]$ $C[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/b/e/fbeb56df8cf1724a777f83396b15495982.png)
и
![$L^2[a,b]$ $L^2[a,b]$](https://dxdy-03.korotkov.co.uk/f/6/c/b/6cb70440b67cc96434676d10a57ac8f582.png)
"руками". Например, если приблизить параболу

линейной на отрезке
![$[-1,1]$ $[-1,1]$](https://dxdy-03.korotkov.co.uk/f/6/9/9/699628c77c65481a123e3649944c0d5182.png)
(в цэ), то получится функция
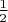
. Эту функцию можно найти путём несложных рассуждений, построив график параболы, а доказать с помощью теоремы про альтернанс. А вот как искать эти самы функции?