Ряды

[Ketsyki]

Здравствуйте. Проверьте, пожалуйста, правильно ли я решил задачи на сходимость рядов.

1. Найти область сходимости ряда

$ \sum\limits_{n=1}^{\infty} e^{n^2 \cdot \sin(\frac{x^2+1}{n})} $

По признаку Коши:

$ \lim\limits_{n \to \infty} (e^{n^2 \cdot \sin(\frac{x^2+1}{n})})^{1/n} = \lim\limits_{n \to \infty} (e^{n \cdot \sin(\frac{x^2+1}{n})}) = e^{x^2+1} $
Не стал расписывать, как находил предел, но Вольфрам дает такой же ответ.

$e^{x^2+1}>1 \ \forall \ x $
Значит области сходимости нет, т.е. ряд расходится $\forall \ x$

2. Найти область сходимости ряда

$ \sum\limits_{n=1}^{\infty} \frac{1}{n(n+1)} \cdot 2^{\frac{n}{4-x}} $

По признаку Даламбера

$\lim\limits_{n \to \infty} \frac{2^{\frac{n}{4-x}} 2^{\frac{1}{4-x}} n(n+1)}{(n+1)(n+2)2^{\frac{n}{4-x}}} = 2^{\frac{1}{4-x}}$

ОДЗ: $x \ne 4$

При $x>4$ ряд сходится
При $x<4$ ряд расходится

3. Исследовать на абсолютную и условную сходимость (тут у меня подозрение, что я списал не правильно, т.к. решение слишком простое)

$\sum\limits_{n=1}^{\infty} \frac{3n^2+n}{n^4+2} \cos(\frac{n}{3})$

$\cos(\frac{n}{3})\le 1$

$ \frac{3n^2+n}{n^4+2} \cos(\frac{n}{3}) \le \frac{3n^2+n}{n^4+2} \le \frac{3n^2+n}{n^4} = \frac{3n+1}{n^3} \sim \frac{3n}{n^3} = \frac{3}{n^2} \sim \frac{1}{n^2} $

$\frac{1}{n^2}$ - сходится, значит ряд сходится абсолютно

4. Найти радиус сходимости и исследовать поведение ряда на радиусе сходимости

$ \sum\limits_{n=1}^{\infty} \frac{(x-5)^{2n+1}}{3n+8} $

$ \lim\limits_{n \to \infty} \frac{|x-5|^{2n+3}(3n+8)}{|x-5|^{2n+1}(3n+11)} = |x-5|^{2} = (x-5)^{2} $

Ряд сходится абсолютно при $(x-5)^{2}<1$, т.е. при $4 < x < 6$

Радиус сходимости $R=1$

Рассмотрим поведение на границах интервала сходимости:

При $x=6$:
$\sum\limits_{n=1}^{\infty} \frac{(1)^{2n+1}}{3n+8} = \sum\limits_{n=1}^{\infty} \frac{1}{3n+8} \sim \frac{1}{n}$ - ряд расходится

При $x=4$:
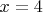
$\sum\limits_{n=1}^{\infty} \frac{(-1)^{2n+1}}{3n+8} = \sum\limits_{n=1}^{\infty} \frac{-1}{3n+8} \sim \frac{1}{n}$ - ряд расходится

Т.е. ряд сходится при $4 < x < 6$.

[Someone]

Вроде бы, правильно. Если я что-нибудь не прочёл так, как хотел прочесть, вместо того, что написано.

[Ketsyki]

Спасибо.

[bot]

Побурчу маленько: для порядку надо бы в 3-м модуль рассматривать.