Опишу промежуточный этап своих поисков. Прошу ногами не пинать, буду рассказывать как физик, на уровне идей, не заморачиваясь особо математической строгостью.
Первый шаг --- перейти от задачи по поиску меры на треугольнике к эквивалентному поиску положительного линейного функционала
![$\Phi[f(x,y)]$ $\Phi[f(x,y)]$](https://dxdy-02.korotkov.co.uk/f/5/2/f/52f176e4002e32c0a292f4936e41e4c082.png)
на непрерывных функциях в треугольнике. Положительного в том смысле, что если


из треугольника, то
![$\Phi[f(x,y)]>0$ $\Phi[f(x,y)]>0$](https://dxdy-02.korotkov.co.uk/f/1/7/9/17968fd7a2fb28c1c6a4bbba9446361e82.png)
. Понятно, что проверять положительность для всех функций --- хлопотное дело. К счастью, существует
теорема Рисса о продолжении, которая гарантирует, что функционал, заданный на подпространстве, можно расширить до функционала во всем пространстве. Для нас это означает, что можно ограничиться подпространством многочленов не выше второй степени,

. Поскольку мы хотим, чтобы средние были равны

, значение функционала на этих функциях очевидно из его линейности
![$\Phi[p_2(x,y)]=\sum_k c_kf_k$ $\Phi[p_2(x,y)]=\sum_k c_kf_k$](https://dxdy-02.korotkov.co.uk/f/d/8/4/d844dfdb3c193261f1d755f415204a8682.png)
. Для положительных на треугольнике многочленов значение функционала должно быть положительным: если

на треугольнике, то

. Описать область

--- вот задача, которую надо решить.
Теперь я расскажу, что написано о решении этой задачи у Крейна и Нудельмана "Проблема моментов Маркова и экстремальные задачи". Нетрудно видеть, что множество положительных функций представляет собой выпуклый конус: вместе с функкцией

ему принадлежит луч

,

, а вместе с функциями

и

--- соединяющий их отрезок

,

. Образующие этого конуса --- лучи тех положительных функций, которые не могут быть представлены как сумма двух других положительных функций.
Если вектор

лежит в конусе, то вектор

, определяемый неравенством

лежит в дуальном конусе, образующие которого направлены вдоль нормалей к поверхности исходного конуса.
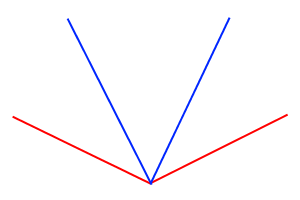
Соотношение дуальности аналогично преобразованию Лежандра или касательному преобразованию: дуальный к дуальному конус совпадает с исходным. Таким образом, для определения области допустимых моментов достаточно найти конус (так называемую коническую оболочку), в котором лежит двумерная поверхность, заметаемая вектором

при изменении

в треугольнике.
К стыду своему должен сказать, что задача эта, вроде бы и не столь уж многомерная (можно еще выкинуть первую, постоянную, компоненту вектора и искать сечение конуса --- выпуклую линейную оболочку), оказалась мне пока не под силу :(
Можно искать конус положительных многочленов, а потом сопрягать. В конце концов у нас многочлены второй степени, линии уровня которых --- кривые второго порядка. Тут нам светит полная ветвлений задача о касании эллипса/гиперболы/параболы с треугольником :) Я пока ничего даже писать не пытался.
Наибольшего продвижения я достиг доморощенным методом, который и описываю ниже.
Подход навеян одномерной задачей. Буду пользоваться механической терминологией и рассуждать нестрого. Попытаемся заменить произвольное распределение масс по треугольнику на распределение, когда массы сосредоточены в конечном числе точек, так чтобы моменты до второго порядка включительно оставались неизменными. Рассуждая физически, начнем со случая, когда масса уже сосредоточена в конечном, но большом числе точек, и посмотрим, нельзя ли это число уменьшить. А потом будем наивно считать, что результат, справедливый для конечного числа точек, остается справедливым и для произвольного распределения массы.
Опыт одномерного случая учит нас, что любое распределение массы на отрезке можно заменить двумя точками, одна из которых лежит в заданном конце отрезка. Из этого наблюдения проистекает замечательная теоремка: систему двух точек можно заменить эквивалентной системой двух точек, расположенных на той же прямой, причем одна из новых точек лежит в заданной точке прямой вне исходного отрезка (а вторая --- внутри. Или наоборот: внутри положение задано, а вовне определяется).
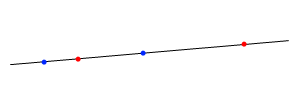
С помощью этого нехитрого приема можно все точки изнутри треугольника, кроме одной, вынести на границы
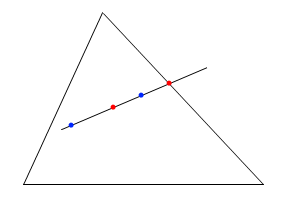
Те же рассуждения для стороны треугольника позволяют все вынести в заданный угол, кроме одной точки. Если я не ошибся нигде с особыми случаями (обычная головная боль математиков :)), то любое распределение масс сводится к такому: одна точка в заданной вершине треугольника, еще две на прилегающих сторонах, и еще одна внутри. В частных случаях "сторонние" точки могут вылезать в углы, а "внутренняя" --- ложиться на сторону. Некоторые массы в частных случаях могут равняться нулю.
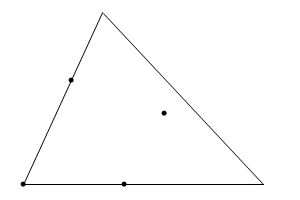
Если внутренняя точка лежит вне треугольника, образованного остальными тремя, то уменьшить количество точек описанным выше приемом уже нельзя. Хотя остается неясно, нельзя ли и в этом случае заменить четыре точки на три.
Ограничения на параметры точек известны: массы неотрицательны, а точки лежат в треугольнике. Обращая зависимость моментов от параметров точек, получаем условия на моменты. К сожалению, так просто обратить нельзя: параметров 7, а моментов 5. Так что в действительности получается условие разрешимости системы неравенств для двух каких-то параметров, например, координат внутренней точки. При таком выборе свободных параметров почти все неравенства сводятся к линейным

и только одно выглядит запутанным

Однако хочу отметить, что это неравенство включает многочлен четвертого порядка.



