Свободные модули

[Chernoknizhnik]

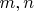
Пусть $A$ - некоторое кольцо (коммутативное, с единицей), $m, n$ - натуральные числа, $f: A^m\rightarrow A^n$ - сюръективный гомоморфизм $A$-модулей. Требуется доказать, что $m\ge n$.
Т.к. $f$ - эпиморфизм, то $A^n$ изоморфно фактормодулю $A^m/\operatorname{Ker}f$. Т.о., последний фактормодуль свободен, а следовательно $A^m$ разлагается в прямую сумму $\operatorname{Ker}f\bigoplus\/A^n$. Вот как отсюда вывести то, что надо? Другими словами: если некоторый (конечнопорожденный) свободный модуль $M$ выделяется прямым слагаемым в некотором другом свободном модуле $N$, то обязательно ли ранг $N$ не менее ранга $M$?
Второй вопрос таков, уважаемые товарищи: если $f$ инъективен, то обязательно ли $n\ge m$? В этой ситуации $A^m$ является подмодулем $A^n$, но прямым слагаемым может и не выделяться, как известно.

[fancier]

Попробуйте воспользоваться тем, что в $A$ существует максимальный идеал $\mathfrak{m}$, т.е. $k:=A/\mathfrak{m}$ -- поле, и попытайтесь свести задачу к аналогичной о векторных пространствах над $k.$

[Chernoknizhnik]

Вот пусть разложили мы $A^m$ в прямую сумму $A^n \bigoplus\operatorname{Ker}f\cong A^m$. В $A$ имеется максимальный идеал $I$, тем самым $A/I$ - поле. Факторизуя $A^n \bigoplus\operatorname{Ker}f\cong A^m$ по $I$, получаем $(A/I)^m\cong (\operatorname{Ker}f\otimes A/I)\bigoplus(A/I)^n$, а значит $(A/I)^n$ - $A/I$-векторное подпространство в $(A/I)^m$. С первой частью, видимо, всё.
А вот с инъективностью не понимаю. Если мы $A^n$ и $A^m$ тензорно умножим на $A/I$, то инъективность может и потеряться. Так может не обязательно во втором случае $n\ge m$?

[fancier]

Chernoknizhnik в сообщении #649482 писал(а):

Вот пусть разложили мы $A^m$ в прямую сумму $A^n \bigoplus\operatorname{Ker}f\cong A^m$. В $A$ имеется максимальный идеал $I$, тем самым $A/I$ - поле. Факторизуя $A^n \bigoplus\operatorname{Ker}f\cong A^m$ по $I$, получаем $(A/I)^m\cong (\operatorname{Ker}f\otimes A/I)\bigoplus(A/I)^n$, а значит $(A/I)^n$ - $A/I$-векторное подпространство в $(A/I)^m$. С первой частью, видимо, всё.

Тут проще воспользоваться тем, что тензорное произведение $\otimes_A(A/I)$ -- точный справа функтор (следовательно, сохраняет сюръективность).

Цитата:

А вот с инъективностью не понимаю. Если мы $A^n$ и $A^m$ тензорно умножим на $A/I$, то инъективность может и потеряться. Так может не обязательно во втором случае $n\ge m$?

Обязательно, посмотрите тут: http://mathoverflow.net/questions/30860/ranks-of-free-submodules-of-free-modules или еще тут: http://mathoverflow.net/questions/136/atiyah-macdonald-exercise-2-11/2622#2622 обсуждение. Идея доказательства в использовании правила Крамера для колец (любые $n+1$ элементов в $A^n$ линейно зависимы).

[Chernoknizhnik]

Спасибо!