Существование элементов существующего множества

[dydx]

epros в сообщении #644455 писал(а):

Теперь $\exists y \forall b (P(b) \to b \in y)$ почему-то заменилось на $\exists y \forall z (\forall b (P(b) \leftrightarrow b \in z) \to z \in y)$. Это зачем?

dydx в сообщении #644405 писал(а):

Я неправильно написал. Я почему-то от вопроса существования элементов существующего множества перешел к вопросу существования подмножеств существующего множества и сразу не заметил этого. Конечно же я не спорю с тем, что подмножества существующего множества существуют, т.е. это очевидно следует из схемы выделения. Прошу прощенья.

epros в сообщении #644455 писал(а):

Чтобы посмотреть что будет, если из объектов со свойством $P$ нельзя собрать множество?

Нет, наоборот: посмотреть, всегда ли можно из объектов со свойством $P$ собрать множество, если... Короче, докажите импликацию $\exists y \forall z (\forall b (P(b) \leftrightarrow b \in z) \to z \in y) \to \exists x \forall b (b \in x \leftrightarrow P(b))$.

[master]

dydx в сообщении #644468 писал(а):

Короче, докажите импликацию $\exists y \forall z (\forall b (P(b) \leftrightarrow b \in z) \to z \in y) \to \exists x \forall b (b \in x \leftrightarrow P(b))$.

$\exists y \forall z (\forall b (P(b) \leftrightarrow b \in z), z=\neg x \to z \in y) \to \neg \exists x \forall b (b \in x \leftrightarrow P(b))$.
если бэ элемент

[epros]

dydx в сообщении #644468 писал(а):

Короче, докажите импликацию $\exists y \forall z (\forall b (P(b) \leftrightarrow b \in z) \to z \in y) \to \exists x \forall b (b \in x \leftrightarrow P(b))$.

Не получится. Я же сказал: Предпосылка - тождественная истина, а следствие - зависит от $P$. Т.е. для некоторых $P$ верно, для некоторых - нет.

Всё ещё не понимаю в чём смысл....

[dydx]

epros в сообщении #644517 писал(а):

Предпосылка - тождественная истина

Докажите.

[epros]

dydx в сообщении #644521 писал(а):

Докажите.

Я же сказал, есть два варианта:

1) $\exists z \forall b ~ P(b) \leftrightarrow b \in z$ и
2) $\nexists z \forall b ~ P(b) \leftrightarrow b \in z$

В первом случае для данного $P$ имеем единственное $z$, откуда следует, что $\exists y ~ z \in y$ для данного единственого $z$.

Во втором случае имеем тождественную истинность $(\forall b ~ P(b) \leftrightarrow b \in z) \to z \in y$ в силу тождественной ложности предпосылки импликации.

[dydx]

epros в сообщении #644535 писал(а):

В первом случае для данного $P$ имеем единственное $z$, откуда следует, что $\exists y ~ z \in y$ для данного единственого $z$.

Согласен.

epros в сообщении #644535 писал(а):

Во втором случае имеем тождественную истинность $(\forall b ~ P(b) \leftrightarrow b \in z) \to z \in y$ в силу тождественной ложности предпосылки индукции.

Не согласен. Как вообще формула со свободными переменными может быть истинной (или ложной)?

[epros]

dydx в сообщении #644555 писал(а):

Как вообще формула со свободной переменной может быть истинной (или ложной)?

Тождественная истинность или ложность означает истинность или ложность при любых значениях свободных переменных.

[dydx]

epros в сообщении #644561 писал(а):

Тождественная истинность или ложность означает истинность или ложность при любых значениях свободных переменных.

Что такое "значение свободной переменной"? У нас в теории есть только символы и их комбинации.

-- 14.11.2012, 20:09 --

Из $\forall z \neg (P(b) \leftrightarrow b \in z)$ следует $\neg (P(b) \leftrightarrow b \in z)$.
Т.к. $\neg (P(b) \leftrightarrow b \in z) \to ((P(b) \leftrightarrow b \in z) \to z \in y)$, то $(P(b) \leftrightarrow b \in z) \to z \in y$.
Так, ok. Я согласен, что формула $(P(b) \leftrightarrow b \in z) \to z \in y$ выводима. Теперь докажите, что формула $\exists y \forall z ~ (P(b) \leftrightarrow b \in z) \to z \in y$ выводима.

[AKM]

Jnrty в сообщении #643743 писал(а):

Эту тему и две параллельных ("Количество множеств" и "Количество натуральных чисел") закрываю как вполне бессмысленные. dydx - предупреждение за троллинг. При повторении будете заблокированы.

Реализую предупреждение коллеги. Блокировка (на две недели пока).

[Someone]

Someone в сообщении #644183 писал(а):

dydx в сообщении #644107 писал(а):

Суть этой темы: докажите, что не существуют формулы $P(b)$ аксиоматической теории множеств такой, что существуют формальные доказательства $Pr_1(P)$ и $Pr_2(P)$.

Если в теории существуют оба указанных Вами доказательства, то теория просто противоречива и не имеет права на существование.

dydx в сообщении #644331 писал(а):

Теория противоречива тогда и только тогда, когда существует высказывание этой теории $\varphi$ такое, что высказывания $\varphi$ и $\neg \varphi$ оба доказуемы. Поэтому, если Вы говорите, что она будет противоречивой, если существует $P(b)$ такое, что существуют $Pr_1(P)$ и $Pr_2(P)$, то докажите существование такого $\varphi$.

Ну зачем мне-то это доказывать? Я не утверждаю, что ZFC противоречива. Это Вы какие-то глупости придумываете, потом начинаете их подправлять, когда глупость вылезает, и так далее. И требуемое Вами $\varphi$ уже Вами же и сформулировано.

dydx в сообщении #644107 писал(а):

Допустим, $P(b)$ - формула аксиоматической теории множеств. И, допустим, есть формальное доказательство $Pr_1(P)$ высказывания $\exists y \forall b (P(b) \to b \in y)$. Возможны три варианта: либо существует формальное доказательство $Pr_2(P)$ высказывания $\neg \exists x \forall b (b \in x \leftrightarrow P(b))$, либо существует формальное доказательство $Pr_3(P)$ высказывания $\exists x \forall b (b \in x \leftrightarrow P(b))$, либо (если только аксиоматическая теория не полна) не существует формального доказательства и высказывания $\neg \exists x \forall b (b \in x \leftrightarrow P(b))$, и высказывания $\exists x \forall b (b \in x \leftrightarrow P(b))$.

Суть этой темы: докажите, что не существуют формулы $P(b)$ аксиоматической теории множеств такой, что существуют формальные доказательства $Pr_1(P)$ и $Pr_2(P)$.

Исходной посылкой у Вас является доказуемость высказывания $\exists y\forall b(P(b)\rightarrow(b\in y))$, следовательно, это высказывание истинно. Оно означает, что все элементы $b$, удовлетворяющие условию $P(b)$, являются элементами некоторого множества. Обозначим $a$ любое такое множество, то есть, $\forall b(P(b)\rightarrow(b\in a))$. По аксиоме выделения $\exists x\forall b((b\in x)\leftrightarrow(P(b)\wedge(b\in a)))$. Поскольку $b\in a$ является следствием $P(b)$, получаем $\exists x\forall b((b\in x)\leftrightarrow P(b))$. Таким образом, высказывание $\varphi\equiv\exists x\forall b((b\in x)\leftrightarrow P(b))$ доказуемо. 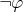Ну, а $\neg\varphi$ - это как раз Ваше $\neg\exists x\forall b((b\in x)\leftrightarrow P(b))$. Поэтому, как я и говорил, Ваше желание иметь оба доказательства $Pr_1(P)$ и $Pr_2(P)$ может осуществиться только в противоречивой теории.

Как я понимаю, основной вопрос этой темы разрешён, так что её можно и закрыть.