Равномерная сходимость функцион. последовательности, ряд

[champion12]

Есть две задачки, которые хотелось бы понять. Дайте, пожалуйста, пару советов по поводу решения!

1) Сходится ли последовательность равномерно на промежутке $(0;+\infty)$?

$f_n(x)=n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)$

Думаю, что лучше проверить это условие:

$\displaystyle\lim_{n\to\infty}\sup_{x\in X} \Big|f_n(x) - f(x)\Big|=0$

Мне кажется, что эта последовательность сходится к $f(x)=0$, так как, если разложить синус в окрестности нуля в ряд Тейлора, то $\displaystyle\lim_{n\to\infty}\dfrac{n}{2^{kn}x}=0\;\;\;\;\;\;\;\;k\in Z$

Ну а как дальше быть?

2) Найти $\displaystyle\sum_{n=0}\dfrac{(-1)^n\cdot 2^{-\frac{n}{2}}}{n+0,5}$

А тут с чего начать - пока что не представляю. Может подскажите? Похоже, что здесь почленное дифференцирование и интегрирование не помогут, на мой взгляд...

[xmaister]

champion12 в сообщении #636420 писал(а):

Мне кажется, что эта последовательность сходится к $f(x)=0$

Не угадали, $\sup_{x\in X} \Big|f_n(x) \Big|=n$.

-- 27.10.2012, 15:56 --

2. Разложение Тейлора логарифма знаете? А что будет с разложением если вычесть $\ln (1+x)-\ln (1-x),|x|<1$

[champion12]

xmaister в сообщении #636457 писал(а):

Не угадали, $\sup_{x\in X} \Big|f_n(x) \Big|=n$.

Спасибо, согласен. Синус по модулю не больше $1$. Может тогда взять $f(x)=n$ ? Или не поможет? То есть по какому принципу выбирать $f(x)$?

xmaister в сообщении #636457 писал(а):

2. Разложение Тейлора логарифма знаете? А что будет с разложением если вычесть $\ln (1+x)-\ln (1-x),|x|<1$

$\ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots = \displaystyle\sum^{\infty}_{n=0} \frac{(-1)^n x^{n+1}}{n+1} $

$\ln(1-x) = -x - \frac{x^2}{2} - \frac{x^3}{3} - \cdots = -\displaystyle\sum^{\infty}_{n=0} \frac{x^{n+1}}{n+1} $

$\ln(1+x)-\ln(1-x)=\displaystyle\sum^{\infty}_{n=0} \frac{(-1)^n x^{n+1}}{n+1} + \displaystyle\sum^{\infty}_{n=0} \frac{x^{n+1}}{n+1}=2\displaystyle\sum^{\infty}_{n=0}\dfrac{x^{2n+1}}{2n+1}}$

[xmaister]

champion12 в сообщении #636513 писал(а):

Спасибо, согласен. Синус по модулю не больше $1$. Может тогда взять $f(x)=n$ ? Или не поможет? То есть по какому принципу выбирать $f(x)$?

Не понял, а что такое $n$? Попробуйте доказать, что эта последовательность не сходится равномерно. Вы знаете, что есть критерий Коши для равномерной сходимости последовательности непрерывных функций (Это означает полноту пространства непрерывных функций с топологией равномерной сходимости). Рассмотрите какое-то $\varepsilon$, например $\varepsilon=\frac{1}{2}$ и попробуйте найти для него $N$, чтобы были соблюдены условия кр. Коши. Или докажите, что такого $N$ попросту нет.

champion12 в сообщении #636513 писал(а):

$\ln(1+x)-\ln(1-x)=\displaystyle\sum^{\infty}_{n=0} \frac{(-1)^n x^{n+1}}{n+1} + \displaystyle\sum^{\infty}_{n=0} \frac{x^{n+1}}{n+1}=2\displaystyle\sum^{\infty}_{n=0}\dfrac{x^{2n+1}}{2n+1}}$

Хорошо! Теперь перепешите $\displaystyle\sum_{n=0}\dfrac{(-1)^n\cdot 2^{-\frac{n}{2}}}{n+0,5}=2\sum_{n=0}\dfrac{(-\frac{1}{\sqrt{2}})^n}{2n+1}$.

[champion12]

xmaister в сообщении #636522 писал(а):

Хорошо! Теперь перепешите $\displaystyle\sum_{n=0}\dfrac{(-1)^n\cdot 2^{-\frac{n}{2}}}{n+0,5}=2\sum_{n=0}\dfrac{(-\frac{1}{\sqrt{2}})^n}{2n+1}$.

Спасибо! Но в той формуле только нечетные степени... Хочется, формально написать $x^{2n+1}=(-\frac{1}{\sqrt{2}})^n$, но у нас $x$ ведь не должно зависеть от $n$ -- потому пока что не знаю - что делать дальше.

-- 27.10.2012, 18:36 --

1)

Критерий Коши для последовательности:
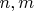
Чтобы последовательность функций $ {f_n}(x)$, определённых на множестве $V$, равномерно сходилась на этом множестве, необходимо и достаточно, чтобы для всякого $\varepsilon>0$ существовал номер $N=N(\varepsilon)$, такой, что при всех $n, m$ больше либо равных $N$, одновременно для всех $x \in V$ выполнялось неравенство $\ \left|{f_n}(x) - \ {f_m}(x)\right| < \varepsilon$

Возьмем $\varepsilon=0,5$

$\Bigg| n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)-m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|<0,5$

Попробуем доказать, что нет такого номера $N$, чтобы выполнялось неравенство выше сразу для всех $x$

$\Bigg| \dfrac{n}{\sqrt{n^2+m^2}}\cdot \sin\Big(\dfrac{1}{2^nx}\Big)-\dfrac{m}{\sqrt{n^2+m^2}}\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|<\dfrac{0,5}{\sqrt{n^2+m^2}}$

Не, что-то здесь не выходит перейти от разности к произведению...(

[xmaister]

1)Докажите, что $\|f_n-f_m\|\ge \|f_n\|-\|f_m\|$.
2)$x=\frac{i}{\sqrt[4]{2}}$

[champion12]

xmaister в сообщении #636566 писал(а):

1)Докажите, что $\|f_n-f_m\|\ge \|f_n\|-\|f_m\|$.
2)$x=\frac{i}{\sqrt[4]{2}}$

1) $f_n^2-2f_nf_m+f_m^2 \ge f_m^2-2\|f_n\|\cdot \|f_m\|+f_m^2$

$-2f_nf_m \ge -2\|f_n\|\cdot \|f_m\|$

$\|f_n\|\cdot \|f_m\|\ge f_nf_m$ (что очевидно)

$\Bigg| n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\Bigg|-\Bigg|m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|\leqslant \Bigg| n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)-m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|<0,5$

А как дальше?

2) $\displaystyle\sum_{n=0}\dfrac{(-1)^n\cdot 2^{-\frac{n}{2}}}{n+0,5}=\ln\Big(1+\frac{i}{\sqrt[4]{2}}\Big)-\ln\Big(1-\frac{i}{\sqrt[4]{2}}\Big)$

А никак нельзя вернуться к вещественным числам?

[xmaister]

champion12 в сообщении #636575 писал(а):

$\|f_n\|\cdot \|f_m\|\ge f_nf_m$ (что очевидно)

Так писать нельзя. Потому что $f_n,f_m$- векторы из $C(0,\infty)$, а $\|\cdot\|:C(0,\infty)\to\mathbb{R}$- функционал. Надо так $\|f_n\|\le \|f_n+f_m-f_m\|\le \|f_n-f_m\|+\|f_m\|$

champion12 в сообщении #636575 писал(а):

2) $\displaystyle\sum_{n=0}\dfrac{(-1)^n\cdot 2^{-\frac{n}{2}}}{n+0,5}=\ln\Big(1+\frac{i}{\sqrt[4]{2}}\Big)-\ln\Big(1-\frac{i}{\sqrt[4]{2}}\Big)$

Тут Вы потеряли множитель. Я попробую избавится от комплексных чисел.

[champion12]

$\displaystyle\sum_{n=0}\dfrac{(-1)^n\cdot 2^{-\frac{n}{2}}}{n+0,5}=0,5\ln\Big(1+\frac{i}{\sqrt[4]{2}}\Big)-0,5\ln\Big(1-\frac{i}{\sqrt[4]{2}}\Big)$

-- 27.10.2012, 19:25 --

xmaister в сообщении #636582 писал(а):

Так писать нельзя. Потому что $f_n,f_m$- векторы из $C(0,\infty)$, а $\|\cdot\|:C(0,\infty)\to\mathbb{R}$- функционал. Надо так $\|f_n\|\le \|f_n+f_m-f_m\|\le \|f_n-f_m\|+\|f_m\|$

А, спасибо, понятно)

$\Bigg| n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\Bigg|-\Bigg|m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|\leqslant \Bigg| n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)-m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|<0,5$

$\Bigg| n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\Bigg|-\Bigg|m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|<0,5$

[xmaister]

champion12 в сообщении #636586 писал(а):

$\Bigg| n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\Bigg|-\Bigg|m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\Bigg|<0,5$

Почти, только $\left\|n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\right\|-\left\|m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\right\|=n-m<0,5$. Что не верно. Отсюда уже сразу видно, что для всякого$N$ найдутся $n,m$, такие что $\|f_n\|-\|f_m\|>\frac{1}{2}$

[champion12]

xmaister в сообщении #636613 писал(а):

Почти, только $\left\|n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\right\|-\left\|m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\right\|=n-m<0,5$. Что не верно. Отсюда уже сразу видно, что для всякого$N$ найдутся $n,m$, такие что $\|f_n\|-\|f_m\|>\frac{1}{2}$

А почему $\left\|n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\right\|-\left\|m\cdot \sin\Big(\dfrac{1}{2^mx}\Big)\right\|=n-m$ ???

Понимаю, что $ -1\le \sin\Big(\dfrac{1}{2^nx}\Big)\le 1$, но это ведь не значит, что $\sin\Big(\dfrac{1}{2^nx}\Big)=1$?

[xmaister]

А что такое $\left\|n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\right\|$? Я наверное Вас совсем запутал. Я обозначал $\|f\|=\sup\limits_{x\in X}|f(x)|$, чтобы набирать поменьше буков. А почему $\sup\limits_{x\in X}|f_n(x)|=n$ Вы разобрались.

[champion12]

xmaister в сообщении #636639 писал(а):

А что такое $\left\|n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)\right\|$?

Это норма. А принципиально здесь использовать именно норму, а не просто модуль? Просто ведь в критерии коши стоит модуль...

Я просто не понял -- как критерий Коши формулируется "на языке норм"

[xmaister]

champion12 в сообщении #636642 писал(а):

А принципиально здесь использовать именно норму, а не просто модуль?

Если Вы просто напишите модуль, то это будет уже не верно. По сути, Вам надо доказать, что последовательность Ваших функций $f_n(x)=n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)$ сходится или расходится в нормированном пространстве $C(0,\infty)$ над $\mathbb{R}$ с нормой $\|f\|=\sup\limits_{x\in X}|f(x)|$. Сходимость рассматривается по норме. Мне, лично, удобнее так понимать равномерную сходимость, чем голое определение на $\varepsilon -\delta$.

[champion12]

xmaister в сообщении #636650 писал(а):

Если Вы просто напишите модуль, то это будет уже не верно. По сути, Вам надо доказать, что последовательность Ваших функций $f_n(x)=n\cdot \sin\Big(\dfrac{1}{2^nx}\Big)$ сходится или расходится в нормированном пространстве $C(0,\infty)$ над $\mathbb{R}$ с нормой $\|f\|=\sup\limits_{x\in X}|f(x)|$. Сходимость рассматривается по норме. Мне, лично, удобнее так понимать равномерную сходимость, чем голое определение на $\varepsilon -\delta$.

Да, чего-то я запутался(((

P.S. А реально в той задаче про $\ln(1+x)-\ln(1-x)$ избавиться от комплексных чисел?

-- 27.10.2012, 22:02 --

$$0,5\ln\Big(1+\frac{i}{\sqrt[4]{2}}\Big)-0,5\ln\Big(1-\frac{i}{\sqrt[4]{2}}\Big)=0,5\ln\Bigg(\dfrac{1+\frac{i}{\sqrt[4]{2}}}{1-\frac{i}{\sqrt[4]{2}}}}\Bigg)=0,5\ln\Bigg(\dfrac{\big(1+\frac{i}{\sqrt[4]{2}}\big)^2}{\big(1-\frac{i}{\sqrt[4]{2}}\big)\big(1+\frac{i}{\sqrt[4]{2}}\big)}}\Bigg)=0,5\ln\dfrac{\big(\sqrt[4]{2}+i\big)^2}{\sqrt{2}+1}$$