Все таки хочу с этим разобраться до конца.
Вообще суть в том чтобы во-первых построить биекцию между всеми векторами одного класса и одним удобным вектором с этого же класса, во-вторых построить биекцию между множеством таких векторов и окружностью радиуса 1.Я правильно понял?
Если это так, то как построить биекции?
Еще пара вопросов
1)В книге Шеня указано, что между

и
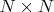
можно построить взаимно однозначное соответствие заданное многочленом второй степени с рациональными коэффициентами.Как его найти?
2)Если существует инъекция из

в

, то существует инъекция из

в

(

означает множество всех отображений из

в

).Это в общем очевидно, но доказательство у меня выходит слишком громоздким, для такой задачи.
3)Доказать, что

.