Всеукраинская студенческая олимпиада, Львов-2007

[dm]

ВСЕУКРАИНСКАЯ СТУДЕНЧЕСКАЯ
ОЛИМПИАДА ПО МАТЕМАТИКЕ
Львов, 18–20 апреля 2007 года
I–II курсы, 1-ый день

1. (В.Андрийчук) Найти все целые числа (не делящиеся на 1000), последние три цифры которых не меняются при возведении в квадрат.

2. (С.Пидкуйко) Пусть $f\in C^{\infty}(\mathbb{R})$ и последовательность $(f^{(n)})$ равномерно сходится на каждом промежутке $[a,b]\subset\mathbb{R}$. Найти $\lim\limits_{n\to+\infty}{f^{(n)}(x)}$.

3. (Я.Мыкытюк) Пусть вещественнозначная функция $f\in C^{2}[0;\pi]$ выпукла. Доказать, что

$$\int_{0}^{\pi}{f(t)\sin t dt}\le\int_{0}^{\pi}{f(t)\lvert\cos t\rvert dt.}$$

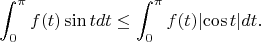
4. (О.Равский) Периодом функции $f:\mathbb{R}\to\mathbb{R}$ будем называть такое число $a\not=0$, что $f(x+a)=f(x)$ для всех $x\in\mathbb{R}$. Пусть $f_1,f_2,f_3:\mathbb{R}\to\mathbb{R}$ — периодические функции, такие, что $f_1(x)+f_2(x)+f_3(x)=0$ для всех $x\in\mathbb{R}$. Верно ли, что некоторые две (разные) из этих функций имеют общий период?

5. (О.Скаскив) Доказать, что

$$\lim_{x\to+\infty}{\frac{x}{\ln x}\sum_{n=0}^{+\infty}{\frac{1}{2007^{n}+x}}}=\frac{1}{\ln 2007}.$$

6. (О.Скаскив) Все корни многочлена $P(x)$ действительные. Доказать, что для каждого $\lambda\in\mathbb{R}$ все корни многочлена $P(x)+\lambda P'(x)$ также действительные.

© Львовский национальный университет им. И.Франко, механико-математический факультет


ВСЕУКРАИНСКАЯ СТУДЕНЧЕСКАЯ
ОЛИМПИАДА ПО МАТЕМАТИКЕ
Львов, 18–20 апреля 2007 года
I–II курсы, 2-ой день

1. (О.Скаскив) Доказать, что

$$0<\int_{0}^{+\infty}{\frac{xdx}{e^{x}-1}}-\sum_{n=1}^{2007}\frac1{n^{2}}<\frac1{2007}.$$

2. (Б.Забавский) Доказать, что если для квадратной матрицы $A$ порядка $2$ существует $n\in\mathbb{N}$ такое, что $A^{n}=0$, то $A^{2}=0$.

3. (О.Скаскив) Пусть $f(x)=\sum\limits_{k=1}^{n}{a_{k}e^{ikx}}$, $f(0)=0$, $a_{k}\in\mathbb{R}$ $(1\le k\le n)$. Если $|f(x)|\le |\sin x|$ для всех $x\in [-\pi/2;\pi/2]$, то $|\sum\limits_{k=1}^{n}{ka_{k}}|\le 1$. Доказать.

4. (И.Гуран) Пусть $K$ — круг в плоскости $\mathbb{R}^{2}$, $C$ — его граничная окружность, $f:\ K\to\mathbb{R}^{2}$ — непрерывное отображение круга в плоскость, являющееся тождественным на окружности $C$. Тогда $f$ принимает все значения в $K$, т.е. $\forall\ q\in K$ существует точка $p\in K$ такая, что $f(p)=q$. Доказать.

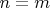
5. (О.Скаскив) Пусть $\alpha_{1}>\alpha_{2}>\ldots>\alpha_{n}>0$ и $\beta_{1}>\beta_{2}>\ldots>\beta_{m}>0$ такие, что $\sum_{k=1}^{n}{\sin(\alpha_{k}x)}=\sum_{k=1}^{m}{\sin(\beta_{k}x)}$ для каждого $x\in\mathbb{R}$. Доказать, что $n=m$ и $(\alpha_{1},\ldots,\alpha_{n})=(\beta_{1},\ldots,\beta_{n})$.

6. (В.Мыхайлюк) Существует ли функция $f:{\mathbb R}^2\to{\mathbb R}$, имеющая в каждой точке непрерывные частные производные первого порядка и не имеющая в каждой точке ни одной частной производной второго порядка?

© Львовский национальный университет им. И.Франко, механико-математический факультет


ВСЕУКРАИНСКАЯ СТУДЕНЧЕСКАЯ
ОЛИМПИАДА ПО МАТЕМАТИКЕ
Львов, 18–20 апреля 2007 года
III–IV курсы, 1-ый день

1. (В.Андрийчук) Найти с точностью до изоморфизма все группы $G$ порядка 2007 с нетривиальным центром.

2. (Т.Банах) Пусть $C$ — замкнутый конус в гильбертовом (более общо, банаховом) пространстве $X$.
a) Доказать, что $C$ имеет основание, если пространство $X$ сепарабельное.
b) Доказать, что $C$ имеет ограниченное основание, если пространство $X$ конечномерное.
c) Обязательно ли $C$ имеет ограниченное основание, если $X$ бесконечномерное?
d) Обязательно ли $C$ имеет основание, если пространство $X$ несепарабельное?
Необходимые определения. Подмножество $C$ банахового пространства $X$ называется конусом в $X$, если: 1) $ax+by\in C$ для произвольных точек $x,y\in C$ и действительных чисел $a,b\ge0$ и 2) $C\cap(-C)=\{0\}$. Подмножество $B\subset C$ называется основанием конуса $C$, если $B$ лежит в замкнутой гиперплоскости, которая не содержит нуля и $C=\{tb:b\in B,\; t\ge 0\}$.

3. (Я.Мыкытюк) Пусть $X$ — банахово пространство и $\mathcal{N}(X)$ — множество необратимых операторов в алгебре $\mathcal{B}(X)$ непрерывных линейных операторов на $X$. Докажите, что

$$dist(A,\mathcal{N}(X))=\frac{1}{\lVert A^{-1}\rVert}.$$

4. (О.Скаскив) Пусть $x\in L_{1},$ и $y\in L_{\infty}$ такие, что $|\int{xyd\mu}|=1$. Доказать, что для каждого $M>0$

$$\|y\|_{L_{1}}\ge\frac1{M}(1-\|y\|_{L_{\infty}}\int\limits_{|x|>M}{|x|d\mu}).$$

Здесь $L_{\infty}=L_{\infty}([0;1],\mu)$, $L_{1}=L_{1}([0;1],\mu)$, $\mu$ — мера Лебега на прямой, $\|y\|_{X}$ — норма в соответствующем нормированном пространстве $X$.

5. (О.Скаскив) Пусть $R(z)=\frac{P(z)}{Q(z)}$, $P$,$Q$ — взаимно простые многочлены, $deg\ R=\max\{deg\ P,\ deg\ Q\}>1$. Доказать, что все нули функции $f(z)=\overline{R(z)}-z$ изолированные.

6. (В.Мыхайлюк) Множество $D$ называется нигде не плотным, если внутренность его замыкания является пустым множеством. Множество $C$ содержится в произведении $A\times B$ нигде не плотных в $\mathbb R$ множеств $A$ и $B$. Может ли ортогональная проекция множества $C$ на некоторую прямую совпадать со всей прямой?

© Львовский национальный университет им. И.Франко, механико-математический факультет


ВСЕУКРАИНСКАЯ СТУДЕНЧЕСКАЯ
ОЛИМПИАДА ПО МАТЕМАТИКЕ
Львов, 18–20 апреля 2007 года
III–IV курсы, 2-ой день

1. (Т.Банах) а) Доказать, что каждый гомеоморфизм единичной окружности $S=\{z\in\mathbb{C}:|z|=1\}$ на себя продолжается до гомеоморфизма единичного диска $D=\{z\in \mathbb{C}:|z|\le1\}$ на себя.
b) Доказать, что каждое топологическое вложение окружности $S$ в комплексную плоскость продолжается до вложения диска $D$ в $\mathbb{C}$.

2. (О.Скаскив) Пусть $y\in L_{\infty}[0;1]$ и $0<\varepsilon\le\|y\|_{L_{1}}/(1+\|y\|_{L_{\infty}})$. Доказать, что тогда

$$\mu\{t\in [0,\ 1]:\ |y(t)|\ge\varepsilon\}\ge\varepsilon.$$

Здесь $L_{\infty}=L_{\infty}([0;1],\mu)$, $L_{1}=L_{1}([0;1],\mu)$, $\mu$ — мера Лебега на прямой, $\|y\|_{X}$ — норма в соответствующем нормированном пространстве $X$.

3. (Я.Мыкытюк) Пусть $\mathcal{M}_{n}$ — линейное пространство всех квадратных матриц $n\times n$ с комплексными коэффициентами. Доказать, что если спектры матриц $A, B\in \mathcal{M}_{n}$ не пересекаются, то отображение

$$\mathcal{M}_{n}\ni X\to F(X)=F_{A,B}(X)=BX-XA$$

является биекцией $\mathcal{M}_{n}$ на себя.

4. (О.Скаскив) Доказать, что каждое решение дифференциального уравнения

$$f''(x)+xg(x)f'(x)+f(x)=0,$$

где $g(x)\ge 0$ для всех $x\in\mathbb{R}$, а) ограничено на $\mathbb{R}$; b) имеет ограниченную на $\mathbb{R}$ производную.

5. (О.Скаскив) Для произвольной квадратной матрицы $A$ определим $\sin A$ с помощью ряда

$$\sin A=\sum\limits_{n=0}^{+\infty}{\frac{(-1)^{n}}{(2n+1)!}A^{2n+1}}.$$

Существует ли $2\times 2$ матрица $A$ такая, что $\sin A=\begin{pmatrix} 1 & 2007 \\ 0 & 1 \end{pmatrix}$ ?

6. (Л.Здомский) Отображение $f:\ X\to Y$ называют липшицевым относительно метрик $d_{X},d_{Y}$, если $(\exists\ M>0)(\forall\ x_{1},x_{2}\in X):$ $d_{Y}(f(x_{1}),f(x_{2}))\le Md_{X}(x_{1},x_{2})$. Если $(X,d)$ — сепарабельное метрическое пространство мощности, меньшей $c=|\mathbb{R}|$, то существует инъективное липшицевое отображение $f:\ X\to\mathbb{R}$. Доказать.

© Львовский национальный университет им. И.Франко, механико-математический факультет

[незваный гость]

1-1. описать могу: $n \mod 1000 \in \{1,625,376\}$. А вот искать все лень.

[Hypokeimenon]

В чем подвох второй задачи второго дня? Казалось бы, $\phi_A(t) | t^n$, $deg(\phi_A(t)) \le 2$ => $\phi_A(t) \in \{ t^2, t \} $ ( $\phi_A(t)$ -- минимальный аннулирующий многочлен $A$ )?

[RIP]

Hypokeimenon писал(а):

В чем подвох второй задачи второго дня? Казалось бы, $\phi_A(t) | t^n$, $deg(\phi_A(t)) \le 2$ => $\phi_A(t) \in \{ t^2, t \} $ ( $\phi_A(t)$ -- минимальный аннулирующий многочлен $A$ )?

Подвох, видимо, в том, что теорема Гамильтона-Кэли предполагается неизвестной. Решение такое. Поскольку $A^n=0$, то $\det A=0$, отсюда $A^2=(a+d)A$, откуда $A^n=(a+d)^{n-1}A$. Вот, собственно, и всё.

P.S. $A=\begin{pmatrix}a&b\\c&d\end{pmatrix}$

[dm]

Hypokeimenon
Особого подвоха нет. Пробралась в олимпиаду стандартная задача. Защитывались любые корректные решения.
Еще не очень понравилось в текстах, например, что на старших курсах задача 4 первого дня и задача 2 второго дня очень похожи. Ну и еще по мелочи.
Я к составлению текстов отношения не имел, только проверял.

[neo66]

dm писал(а):

1-2 курсы, 1-й день
6. (О.Скаскив) Все корни многочлена $P(x)$ действительные. Доказать, что для каждого $\lambda\in\mathbb{R}$ все корни многочлена $P(x)+\lambda P'(x)$ также действительные.

Можно считать, что $\lambda\neq 0$.
Пусть $P(x)=(x-a_1)^{b_1}\dots (x-a_n)^{b_n}$, где $a_i\in\mathbb{R}, b_i\in\mathbb{N}.$Тогда $P(x)+\lambda P'(x)=\lambda P(x)(\frac{b_1}{x-a_1}+\dots + \frac{b_n}{x-a_n}+\frac{1}{\lambda})$. Нетрудно понять, что требуемое утверждение эквивалентно тому, что уравнение $\frac{b_1}{x-a_1}+\dots + \frac{b_n}{x-a_n}+\frac{1}{\lambda}=0$ имеет ровно $n$ действительных корней. А это очевидно .

[Dandan]

neo66 писал(а):

А это очевидно .

Да ну ? $-/+$

[neo66]

Да, если посмотреть на знак производной левой части и попробовать нарисовать график. Это несложно.

[Pyphagor]

Задача 3. Выпукла вверх или вниз?

[RIP]

Когда говорят просто "выпукла", то подразумевают "выпукла вниз".

[Someone]

RIP писал(а):

Когда говорят просто "выпукла", то подразумевают "выпукла вниз".

Я встречал термины "выпуклая"="выпуклая вверх" и "вогнутая"="выпуклая вниз". А также наоборот. Поэтому очень не люблю их употреблять.

[bot]

незваный гость писал(а):

:evil:
1-1. описать могу: $n \mod 1000 \in \{1,625,376\}$. А вот искать все лень.

Дык, это все и есть.
Так как x и x-1 взаимно просты, то возникает 4 случая, но один из них исключён условием. Чтобы не решать три китайские системы, используем в ней для правых частей параметры $(a,b) \in \{(0,1), \ (1,0), (1,1) \}$
и получаем $x=376 b - 375 a$

[Хорхе]

А как этот интеграл

$$\int_{0}^{+\infty}{\frac{xdx}{e^{x}-1}}.$$

посчитать без комплексного анализа? Я считаю так: замена $x^2$ на $t$ и стандартно, разрезая плоскость вдоль положительных действительных и интегрируя по контуру...

[ИСН]

Развалить в ряд, типа $\int x(e^{-x}+e^{-2x}+e^{-3x}+...)dx$

[Macavity]

neo66 писал(а):

А это очевидно .

Да ну.. А Вы не могли бы немного поподробней?