ton007 писал(а):
А вот общее решение уравнения x````+4=0 как найти? Если когда решаешь, получается под корнем -2i, и 2i, то как общее решение записать?
Паре (простых) сопряжённых корней характеристического уравнения

(

) соответствует пара линейно независимых решений

и

. Просто досчитайте
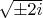
до конца.