А отрицание
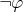
утверждает, что один из элементов графа не связан ни с каким другим, а все остальные элементы парные.
Один единственный:

в формуле

.
Восклицательный знак, кстати, в языке исчисления предикатов изначально отсутствует. Но это не проблема, ибо исчисление с равенством

Сейчас ещё раз всё проверил и убедился, что у меня всё правильно написано. Странно, что у Вас до сих пор вопросы. Идею я изложил, формулы аккуратно выписал. Если всё ещё что-то непонятно, спрашивайте в конкретных местах.
Насчёт единственности "изолированного

". Ну да он само собой будет единственным. Парный элемент не может быть изолированным, изолированный не может быть парным, а я пишу, что существует изолированный элемент, такой, что все отличные от него элементы - парные. Смотрите внимательнее!
На самом деле задача очень простая. Я на экзамене часто подобную даю: придумать предложение, которое будет истинно на конечных моделях произвольной чётной мощности и ложно на всех моделях с нечётным числом элементов. Правда, там чуть легче, поскольку сигнатуру предлагается придумать самостоятельно. Ну и самое простое решение: берём функциональную сигнатуру с одним символом одноместной функции и пишем

Ну а здесь, поскольку был нужен именно граф, надо было, чтобы воспользоваться этой идеей, прописать, что граф задаёт функциональное отношение. Плюс ещё один "левый" элемент добавить, поскольку требуется выразить не чётность, а, наоборот, нечётность.



