1) Найти все натуральные

, для которых числа Каталана

нечетные.
2) Для каких натуральных

существует множество из

последовательных натуральных чисел таких, что наибольшее из этих чисел есть делителем НОК остальных чисел? При каких

такое множество единственное?
3) Для положительных чисел

, таких, что

, доказать неравенство:

4) Четырехугольник

вписан в окружность с центром в точке

. Пусть

-произвольная точка внутри четврехугольника

,

-центры окружностей описанных вокруг треугольников

соответственно. Доказать, что середины отрезков

лежат на одной прямой.
5) Найти все функции

, если известно, что для любых положительных

исполняется

, и существуют такие положительные константы

, что

6) Остроугольный треугольник

вписан в окружность с центром в точке

и радиусом

. Прямая

пересекает окружность, описаную вокруг треугольника
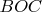
в точке

,

пересекает окружность, описаную вокруг треугольника

в точке

,

пересекает окружность, описаную вокруг треугольника
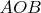
в точке

. Доказать, что

.
7)Задани три паралельные отрезки

, которые не лежат в ондой плоскости. Пусть

- точка пересечения плоскостей

, а

- плоскостей

. Доказать, что

паралелен

.
8) На шахматную доску

положили несколько плиток домино, так, что положить еще одну такую плитку невозможно, если не двигать уже положенные и не ложить плитки друг на друга. Доказать, что свободных клеток на доске осталось не больше чем

.
9) Существуют ли 5 паралелограмов с разными острыми углами, каждый из которых можна составить из трех разных равнобедренных треугольников?
10) Доказать неравенство




