Why, Susskind's lectures are full of examples, unless you were expecting something like explicit functions solving the discussed equations. Then yes, known explicit solutions are not many. I can quote you one, the embedding of a curved spatial section of a curved spacetime of the 'same' physical system - a ball of constant density (not really same because the ball is distorted) - into Euclidean space (MTU Box 23.2 (4)):
![$$z(r)=\left\{\begin{array}{lll}
\sqrt{\dfrac{R^3}{2M}}\left[1-\sqrt{1-\dfrac{2Mr^2}{R^3}}\right]&\qquad&\text{for \(r\leq R\),}\\
\mathstrut&&\\
\sqrt{\dfrac{R^3}{2M}}\left[1-\sqrt{1-\dfrac{2M}{R}}\right]+\sqrt{8M(r-2M)}-\sqrt{8M(R-2M)}&\qquad&\text{for \(r\geq R\),}
\end{array}\right.$$ $$z(r)=\left\{\begin{array}{lll}
\sqrt{\dfrac{R^3}{2M}}\left[1-\sqrt{1-\dfrac{2Mr^2}{R^3}}\right]&\qquad&\text{for \(r\leq R\),}\\
\mathstrut&&\\
\sqrt{\dfrac{R^3}{2M}}\left[1-\sqrt{1-\dfrac{2M}{R}}\right]+\sqrt{8M(r-2M)}-\sqrt{8M(R-2M)}&\qquad&\text{for \(r\geq R\),}
\end{array}\right.$$](https://dxdy-04.korotkov.co.uk/f/b/0/4/b040a916ed6068add64b778e0ef650dc82.png)
You can feed it to a 3d grapher if you want.
For Poisson's equation...
First of all, differential equations don't have some single solution. That's because differentiation lose some information about a function being differentiated. Compare, when you solve an equation
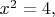
you have two roots because squaring loses information about the sign. For differential equations, you have
infinitely many solutions. To choose just one of them, you have to add some additional conditions, which are not differential equations by themselves (usually), but help to get rid of that infinity. They are called initial conditions, boundary conditions etc. When the main DE is coupled with proper conditions, it is called a
problem. So, when you said that the density is fixed, you didn't yet set the problem, and answers can still be many.
Then, let's move by steps. Poisson's equation is a second-order

-dimensional equation, so let's see first, what is a 1-dimentional second-order DE, and what can be its solutions. I'll take that particular DE (it is not that
any second-order DE looks like this):
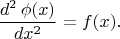
And let's set

to be a constant
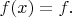
Then, one possible solution is
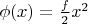
- check it. But it is not unique. If we add 1 to it, then that will be a solution as well, and we can do that as many times as we please. Also we can add

to it, and again arbitrary many times. Actually, the full solution of that
equation (not a
problem yet) would be
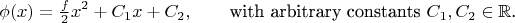
If we want to get only one function, we have to pose additional conditions, like known values of
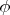
in some points, or of its derivatives. For example, this is a correct
problem for that equation:
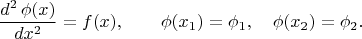
Now we can substitute
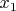
and
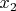
into that solution formula, and find particular values of
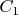
and
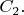
That will make a solution to the problem.
For the actual Poisson's equation, it's

-dimensional, and the freedom for its solutions is much larger, and what problems can be set to it - is covered by a whole new chapter of DE theory - called PDE theory, or classical equations of mathematical physics. I won't get into detail, and just say that for the 3-dimensional equation
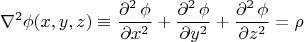
with the constant right hand part, the general form of a solution looks like
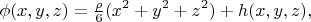
where
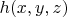
is a function chosen with very much freedom, though not fully arbitrary, and its particular possible forms are described in textbooks. The set of possible functions
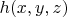
is defined by that

and it bears a special name of
harmonic functions. A possible example is
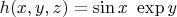
(check again, if you know partial derivatives). So, these functions can change the form of a solution greatly, making it, for example,
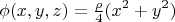
(much less symmetric to the eye than the earlier formula, but actually being just the sample of it).
If I'd wish to set a problem for Poisson's equation, I would have to set a domain, finite or infinite, set a function of density inside that domain, and
set values of 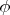 at the boundaries of the domain
at the boundaries of the domain (even in the infinite points). This is one possible kind of problems. So, you may ask what if density is constant, and then
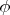
is zero on the boundary of some ball? Then I would answer unambiguously,
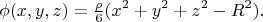
And you've seen this formula before, in
post599164.html#p599164 .



