Хотел задать вопрос. Но пока сочинял пост, сам всё доказал.

Результатом доволен и хочу поделиться, вдруг кому-нибудь будет интересно.
Под полной производной я буду понимать линейное отображение, применяемое к приращению аргумента:
http://en.wikipedia.org/wiki/Total_deri ... linear_map.
Пусть
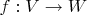
- функция из нормированного векторного пространства в нормированное векторное. Если

дифференцируема в точке

в смысле полной производной, то она дифференцируема в

по любому направлению. Причем производная

в точке

по направлению вектора

(как вектор в

) есть значение полной производной в точке

(как линейного отображения из

в

), примененной к вектору

.
Это можно доказать напрямую, как, например, здесь:
https://people.maths.ox.ac.uk/tillmann/background-multvar.pdf. Но хочется вывести это из теоремы о производной сложной функции.
Сперва докажем лемму (полезную и вне данного контекста): Пусть
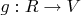
- функция из вещественной прямой в произвольное нормированное векторное пространство, aka вектор-функция. Если

дифференцируема (в смысле полной производной) в точке

, то ее производная в этой точке есть отображение
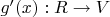
вида
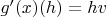
, где

- некоторый постоянный вектор из

. (Так как существует взаимно однозначное соответствие между такими отображениями и векторами из

, то можно считать, что производная - это просто вектор из

. В частности, производная обычной вещественнозначной функции вещественной переменной - это просто число.)
Доказательство:
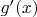
есть по определению линейное отображение из

в

. Из линейной алгебры мы знаем, что
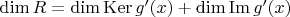
. Так как
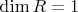
, имеем
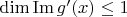
. Если
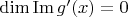
, то всё совсем просто. Если
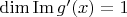
, то в
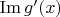
существует базис из единственного вектора

, и тогда
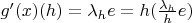
для любого

. Так как
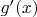
линейно,
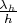
не зависит от

, то есть
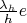
и есть искомый вектор

.
Теперь докажем нашу теорему. Производную

в точке

по направлению

можно представить как
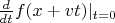
, то есть в виде производной композиции функций
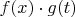
в точке

, где
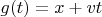
- функция из

в

. (В силу доказанной леммы, линейное отображение, задаваемое полной производной этой композиции функций, можно считать вектором, задаваемым производной по направлению.) По теореме о производной сложной функции, эта производная есть
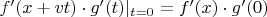
при условии, что производные

и
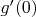
существуют.
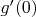
существует и есть отображение
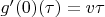
, что нетрудно проверить.

существует по условию. Тогда
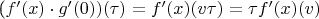
, то есть
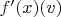
- искомый вектор из леммы, соответствующий данному отображению.
P.S. Идея доказательства не моя, а отсюда:
http://narod.ru/disk/6700950001/Timorin-analiz-24-02-2011-lect3.mp4.html. Однако я при просмотре лекции застопорился на заключительном этапе доказательства, который мне пришлось додумывать самому (в частности, формулировать и доказывать вышеприведенную лемму). Собственно говоря, я здесь привел доказательство из этой лекции, но более разжеванное, для нубов вроде меня.