Имеется выпуклый

-угольник. Два игрока по очереди проводят в нём диагонали, так чтобы новопроведённая не пересекала ни одной из проведённых ранее во внутренних точках (в вершинах, естественно, можно). Тот, кто не сможет сделать ход, - проиграл. Есть ли у кого-то из игроков выигрышная стратегия - и, если да, то какая она?
Ну, в выпуклом

-угольнике можно провести не более чем
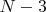
непересекающихся во внутренних точках диагонали (если все исходят из одной вершины). Если бы игроки рисовали их только так (из одной вершины), можно было бы связать исход игры с количеством вершин и чётностью числа
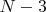
, а в общем случае пока не понимаю, как решать. Надеюсь на Ваши идеи.
P.S.
Может, можно ещё попробовать как-то воспользоваться тем, что любая диагональ разбивает исходный многоугольник на два других - и, если как-то один из игроков будет это деление проводить, что-то да выйдет?



