sadomovalex писал(а):
Someone
то, что Ваше решение совпало с частным случаем, вселяет оптимизм. Не могли бы Вы привести свое решение?
Очень похоже на Ваше, только я сразу шёл к интегралу.
Рассмотрим "треугольник"

, где

- вершина конуса,

,

. Тогда, пренебрегая членами второго порядка малости по

, имеем

,

,

. "Треугольник"

следует развернуть на плоскость. Опустим высоту

на сторону

. Считая угол

очень малым, с точностью до членов второго порядка малости получаем

,

,

и, наконец,

. Вычисление площади по формуле Герона после опускания членов более высокого порядка малости даёт тот же результат.
Осталось написать

.
Добавлено спустя 5 минут 29 секунд:ИСН писал(а):
Someone, у Вас член с синус квадратом под корнем не лишний ли часом?
Скорее всего, Вы не учли, что отрезок

не является высотой

, если
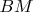
(или

) принять за основание (или наоборот:
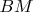
не является высотой, если

принять за основание). Там угол довольно далёк от прямого.