Связи между линиями уровня и максимумом, к счастью, нет никакой.

Что такое
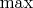
? Это такая штука, которая из двух значений выбирает большее.
В каких-то точках

большим будет

.
А в каких-то точках

большим будет

.
Например, в точке

большим будет ... первое или второе? А в точке

?
Получается, что вся плоскость разбивается на две области: ту, где больше будет

, и ту, где больше будет

.
Как легко догадаться, на границе областей эти выражения будут равны. Это подсказка к тому, как найти границу между этими областями.
А когда нашли границу, то в каждой из областей всё однозначно!