Из книжки Полчинского про теорию струн.
Cohomology in any vector space with a nilpotent operator Q (one such that Q^2 = 0), the kernel of Q modulo the image of Q. That is, the space of closed states (those annihilated by Q) with the exact states (those of the form
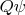
) defined to be equivalent to zero. De Rham cohomobgy is the cohomology of the exterior derivative d acting on differential forms. On a complex manifold, Dolbeault cohomology is the cohomology of

and
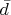
(the (1,0) and (0,1) parts of d) on (p, q)-forms. Homology is the cohomology of the boundary operator. BRST cohomology is the cohomology of the BRST operator, and defines the physical space of a gauge-invariant theory.



