Общее свойство золотого и равностороннего треугольника?

[Nikolai Moskvitin]

Здравствуйте, уважаемые коллеги!

Меня немного озадачил результат, полученный в ходе исследования: выяснилось, что золотой и равносторонний треугольники имеют общее свойство. Сначала скажу, что такое золотой треугольник, затем скажу свойство.

Золотой треугольник- это треугольник с углами 72,72,36.

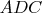
Свойство: обозначим треугольник $ABC$. Пусть $AB$ -основание. Отметим на боковой стороне точку D. Тогда описанная окружность треугольника $ADC$ проходит через центр описанной окружности треугольника $BDA$.
В результате применения теоремы Птолемея и усиленной теоремы синусов получил следующее отношение синусов углов при основании и при общей вершине боковых сторон : $\sin{a}=\sin{2b}$. Так как $\sin x=\sin(180-x)$ и при этом a и b - углы треугольника, получается два различных решения. (Поясню так же, что треугольники обязательно равнобедренные, в чём можно убедиться, если рассмотреть частный случай с высотой). Не ошибся ли я?

Аргумент против: у равностороннего утверждение будет верным для любой пары сторон, у золотого не для любой.
Аргумент за: я мог не учесть какого-нибудь условия, в результате которого один случай исключается.

И ещё: кто какие следствия придумает из этого утверждения, если только оно верно?

[nnosipov]

Nikolai Moskvitin в сообщении #573645 писал(а):

Свойство: обозначим треугольник $ABC$. Пусть $AB$ -основание. Отметим на боковой стороне точку D. Тогда описанная окружность треугольника $ADC$ проходит через центр описанной окружности треугольника $BDA$.

(Видимо, предполагается, что точка $D$ принадлежит стороне $BC$.) Это свойство действительно имеет место (и останется справедливым, если даже считать точку $D$ принадлежащей прямой $BC$).