Возникла проблема с переводом задачи:
Consider a compact Riemann surface

and non-contractible simple loop

on it. Because of non-contractibility, the difference
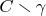
is connected and has a boundary which is homeomorphic of two disjoint circles. Sealing the two holes by topological disks results in a new surface
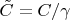
called pinching of

along

.
Compare the Euler characteristic of

and
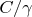
.
Не понимаю, что мы делаем в предложении "Sealing the two holes by topological disks ..." . Отождествляем полученные после выкидывания петли диски?
Интуитивно тогда кажется что род полученной поверхности уменьшится на 1 и эйлерова характеристика увеличится на 2. Я особо не знаком с алгебраической геометрией, знаю только несколько фактов, а общей картины нет..