В то же время я всегда думал, что

разъединять нельзя, так как

ясно показывает,
что именно изменяется в данном случае из аргументов функции. Или может быть есть случаи когда нельзя, а когда можно? Тут же находится вопрос о производных высшего порядка. Например запись:

Показывает нам производную высшего порядка. Зачем писать

в числителе и занаменателе, для того что бы позже иметь возможность разделить их как в вышеприведенном примере с интегрированием подстановкой? Тогда

означает БМИ

...или это есть БМИ

возведенного в степень

?
Как вы уже, наверное, выяснили,

- это не бесконечно малая, а дифференциал. Можно рассматривать как произвольное приращение независимой переменной

.

уже будет линейной частью приращения функции, отвечающей этому приращению

(можно рассматривать как функцию от

и приращения

).
В случае взятия производной от функции одной переменной

можно спокойно разделять на отдельные

и

и переставлять их туда или обратно, то есть, производную можно представить как отношение двух дифференциалов (даже если

- зависимая переменная). Однако, если у вас функция от нескольких переменных

, например, то производная по какой-либо переменной (частная производная)

уже является цельным символом и разделять его нельзя.
Производные высшего порядка, скажем, второго -

. По сути, это что-то вроде

(то есть, оператор

берётся дважды, второй раз - от результата первого раза), а

- это просто сокращённая запись. В случае, если

- независимая переменная, можно взять отдельно дифференциал второго порядка
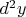
от

и квадрат дифференциала

от

, и поделить - получится вторая производная

по

. В случае, если

не является независимой переменной (а функцией от какой-либо другой переменной) - это уже не верно.



