Я еще и объяснил, почему
изначальный интеграл из вашей статьи по
любому контуру в

сводится к

интегралам Коши. И действительно получается ваш результат. Я не исключаю, что Вы доказали его другим методом (или думаете, что доказали --- к математике там тоже можно придраться). Но, тем не менее,
тот же изначально интеграл вычисляется тривиально более простым способом, и получается тот же ответ. На самом деле если у вас ответ не такой с точностью до замены базиса, то я уверен, что у вас ошибка.
Давайте проверим эту уверенность. Но не Вашим методом, опирающимся на а'приорное "знание", что задача решается в одно действие и контур заданный двумя двумерными замкнутыми проекциями приводит к в точности такому же результату, что дает и фиксированный четырехмерный контур, а нашим более длинным, но последовательным обходом именно четырехмерного контура. В конце концов, на двумерных проекциях запросто могут быть самопересечения, которых нет в четырехмерии. Давайте зафиксируем в четырехмерии простой (но принципиально четырехмерный) контур, который приводит к формуле Коши вида (26-27). А затем покажите какой конкретно заменой базиса,
тот же самый контур приведет к превращению формулы Коши в принципиально иной вид (28-29). Подозреваю, что если такой фокус и имеет место, то исключительно за счет Вашего "контрабандного" и тривиального приема в "доказательстве". Возможно, за счет неразличимости в проекциях контуров с четным и нечетным количеством самопересечений на этих самых проекциях. В любом случае такой, "натурный" эксперимент и именно нашим длинным путем, расставил бы все по своим местам. В частности, есть ли разница для бикомплексного пространства в задании замкнутого контура явно или в виде двух проекций с возможными самопересечениями.
Цитата:
Мы решали одну и ту же задачу --- вычислить интеграл. Эта задача тривиальна.
Есть еще одна причина подойти к вопросу эквивалентности нашего сложного и Вашего "простого" метода получения формул Коши в пространстве бикомплексных чисел. Она заключается в следующем наблюдении. Раз, как Вы утверждаете, получающиеся "4-мерным пространственным путем" формулы полностью эквивалентны в одном из случаев формуле Коши на проективной плоскости с метрикой комплексной переменной, значит, есть резоны предположить, что и второй необычный вид формулы Коши с делителями нуля так же следствие работы метода проекций, только в этом случае на плоскость двойных чисел. Где, как Вы выше утверждали аналога формулы Коши в принципе нет. А мы подозреваем, что есть и теперь даже явно предъявляем этот подозреваемый гипреболический вариант формулы Коши. Он в формулах вида: (28-29) с делителями нуля. Тем более что этот результат очень подозрительно похож на тот, что я получил из эвристических соображений с экспоненциальными формами представления двойных чисел. Таких совпадений не бывает. Вернее, крайне редко..
Давайте попробую заинтересовать Вас так. Если в результате предложенной мною проверки Вы убедитесь, что никакой заменой неизотропного базиса, в котором получены формулы (26-29) первая пара не превращается во вторую, значит, гипотеза о том, что вторая пара формул связана с аналогом формулы Коши на плоскости двойной переменной весьма и весьма резонна. Согласитесь, это был бы достойный и вряд ли тривиальный результат. На сколько я понял, существование гиперболического аналога формулы Коши лично для Вас было бы весьма убедительным аргументом в эквивалентности ТФКП и еще недостроенной ТФДП.
И еще. Вы считаете формулу Коши вида (28-29) тривиальным результатом. Значит, он уже был кем то наверняка получен и Вам не составит труда привести конкретную ссылку, где именно такой вид формулы Коши с делителями нуля уже фигурировал. Чем черт не шутит, может народ уже и формулу Коши не только для бикомплексных, но и для двойных чисел и именно в таком виде получил..
-- Ср апр 25, 2012 21:35:32 --Я, кстати, хотел бы уточнить. Если дан контур в

, то он на самом деле однозначно определяет направление обхода в каждом из

. Поэтому никаких

формул Коши здесь нет, есть одна, именно для этого контура.
Вот именно, для фиксированного контура и с фиксированным правилом его обхода формула Коши всегда одна и для бикомплексных чисел в "ортонормированном базисе" одна из четырех, перечисленных в формулах (26-29). Как раз этот факт я и имел ввиду, когда говорил, что такой результат при фиксированном контуре не изменить никакими изменениями в базисе.
Цитата:
Можно говорить, что их

в том смысле, что выполняется один из

вариантов выбора знака, и мы заранее не знаем, какой. Но тогда, если дан произвольных контур, не пересекающий делители нуля, то его проекции на компоненты могут обходить полюс несколько раз, и даже могут ни одного раза. В обычной формуле Коши такой проблемы не возникает, потому что контур там предполагается несамопересекающимся. Проекция несамопересекающегося контура в

на компоненту может стать самопересекающейся.
Выше я предположил возможность причин проблемы именно в кажущихся пересечениях на двумерных проекциях не самопересекающегося четырехмерного контура.
Цитата:
Т. е. правильная версия формулы Коши в
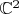
--- это то, что интеграл по контуру равен

, где

и

--- целые числа, равные числу обходов вокруг полюса проекций контура на компоненты.
Да, причем полагаю, много раз можно обходить точку не только евклидовыми полными оборотами, но и псевдоевклидовыми "полными оборотами", поэтому и в формулах с делителями нуля так же должна быть периодичность.
Цитата:
Тем не менее, это тоже достаточно тривиально. В Вашем доказательстве, видимо, неявно используется условие на то, что каждая проекция обходит точку ровно один раз в том или другом направлении.
Да.
Цитата:
Собственно, у Вас неточность, как мне кажется, в формуле (14). При полном обходе угол может меняться на любое кратное кратное

.
Вы скажете, что контур

можно был выбирать произвольно, и можно выбрать, чтобы он обходил точку один раз. На самом деле так нельзя: контур

должен быть непрерывной деформацией контура

, а контуры с разными наборами

нельзя продеформировать друг в друга. Т. е. в этом "модельном" контуре число обходов все равно должно быть таким же, как и у

.
Так я и против этого и не возражаю (не знаю, как соавтор), более того, добавил бы еще периодичность "намотки полных оборотов" еще и псевдоевклидова типа..