Для начала насчет магнитостатики. Я не вижу между ней и электростатикой (в двумерном случае) никакой принципиальной разницы. Все это разговоры о двумерном уравнении Лапласа. В физических постановках естественными для них будут разные типы краевых условий (хотя, опять же, зависит от материалов), но до таких тонкостей, как я понимаю, в данном случае речь не доходит.
Математически разница может быть и не большая. Для двумерной электростатики, в частности, аналитическая функция задающая комплексный потенциал поля одиночного точечного источника имеет вид:

А функция задающая поле одиночного точечного вихря имеет несколько иной вид:

То есть, двумерная электростатика отличается от двумерной магнитостатики примерно так же как вещественные числа отличается от чисто мнимых, а на образах течений идеальной жидкости - как поле с двумерными точечными источниками отличается от полей с двумерными точечными вихрями. Неужели будете настаивать, что с точки зрения физики разницы нет? К тому же есть еще и двумерная электромагнитостатика. Ей, образно выражаясь, можно поставить в соответствие уже не просто вещественные или чисто мнимые числа, а полноценно комплексные. На языке гидродинамики такой ситуации соответствуют течения идеальной жидкости не с источниками и вихрями по отдельности, а вихреисточники и производные от них мультиполи.
Цитата:
Что лично я думаю по поводу аналога соленоидальности. Ну, насколько я понял, это примерно то же, что понятие

-аналитичности. Насколько я понял из обсуждения предыдущей темы (и в некоторые статьи я при этом тоже заглядывал), Вы делаете следующие: вот есть уравнение Лапласа. У него есть решения, соответствующие аналитическим функциям. Потом Вы строите аналоги этих аналитических функций для "двойной переменной", ограничиваясь только элементарными функциями. И говорите, что у получившегося объекта не может не быть физической интерпретации.
Правильно поняли, только элементарными функциями для двойной переменной можно не ограничиваться. Просто поля связанные с элементарными функциями наиболее наглядны и именно с них нужно начинать геометрическую и физическую интерпретацию возможностей функций двойной переменной. В частности, утверждается, что функция двойной переменной

имеющая вид:

задает комплексный потенциал некоего точечного источника уже не на евклидовой, а на псевдоевклидовой плоскости. Другими словами, это псевдоевклидов аналог точечного двумерного "электрического" заряда, или иначе выражаясь, гиперболический заряд двумерного пространства-времени.
Продолжая эту логику, функцию вида

,
где

- гиперболически мнимая единица двойных чисел. Векторное поле, соответствующее такому гиперкомплексному потенциалу и есть простейший псевдоевклидов аналог простейшему соленоидальному полю точечного вихря на евклидовой плоскости. Иными словами, такой гиперкомплексный потенциал задает поле двумерного гиперболического монополя.
Мой вопрос о соленоидальности на плоскости двойной переменной относился именно к такому простейшему полю. Его аналоги силовых линий не концентрические окружности, а концентрические гиперболы. И мне было интересно, что Вы на счет таких двумерных полей могли бы сказать конкретного. Может еще раз попробуете?
Вы что, и правда не видите разницы между парой векторных полей на псевдоевклидовой плоскости, одно из которых источникового, а второе гиперболически вихревого типа?
Я еще могу понять сомневающихся, а то и уверенных в отрицательном ответе на вопрос: имеется ли для таких двумерных гиперболических источников и вихрей реальные четырехмерные прототипы? В конце концов, эту дилемму решат натурные эксперименты. Но понять отказывающихся исследовать соответствующие простейшие математические и геометрические объекты псевдоевклидовой плоскости - понять не могу. А ведь именно это Вы, по сути, и делаете, отказывая соответствующим исследованиям в праве иметь фундаментальную математическую мотивацию. А отказывая в математической мотивации таких исследований, Вы автоматически отказываетесь и от возможной физической мотивации для постановки задачи по поиску и четырехмерных физических аналогов уже четырехмерным гиперболическим источникам и вихрям.
Попробуйте не сходу рубить, мол, это все ни на чем не основанные ожидания, а спокойно посмотреть чуть дальше. Ведь дело, естественно не в двумерии, не важно какое оно: евклидово или псевдоевклидово. Основной вопрос в существенно более близких к реальности четырехмерных конструкциях.
Известно, что комплексные числа и комплексный потенциал на них не расширяются с сохранением всех своих замечательный свойств на три евклидовых или четыре псевдоевклидовых измерения. На этот счет есть замечательная теорема Фробениуса. Но она ничего не запрещает для многомерных расширений коммутативного кольца двойных чисел. Уверен, если бы такие расширения до четырехкомпонентных гиперчисел приводили к геометрии пространства Минковского, мы бы с Вами сейчас не дискутировали по поводу наличия/отсутствия мотиваций, а во всю использовали бы соответствующую алгебру и связанный с нею гиперкомплексный потенциал для решения вполне физических задач. Но именно такое расширения двойных чисел и не возможно. Зато ничто не запрещает иное их расширение, причем без какого бы то ни было ущерба для главного качества двойных чисел и связанной с ними геометрии псевдоевклидова пространства-времени. Речь об имеющемся тут бесконечном множестве глобальных конформных преобразований. Причем только из невырожденных таких расширений на сегодня известно три варианта. Одно из них дает алгебру четверных поличисел, являющуюся прямой суммой четырех вещественных алгебр. И точно так же как с самими двойными числами естественным образом связывается геометрия (а я утверждаю, что и физика) двумерного пространства-времени, точно так же с четверными поличислами естественно и просто связывается геометрия (осмелюсь предпологать, что и физика) четырехмерного пространства-времени. Только метрика соответствующего пространства тут получается не та, которую кому-то хотелось бы видеть, то есть:

а, на первый взгляд, совершенно не физичная, имеющая в базисе аналогичном ортонормированном базису пространства Минковского, просто устрашающе длинный вид:

Спрашивается, можно ли именно из этой метрики извлечь что ни будь ценного как в математическом плане, так в геометрическом, а при возможности, еще и в физическом? Вы говорите, что нельзя. Фигово, мол, то-то, то-то и то-то. Я и мои товарищи утверждаем, что можно. Более того, многое во всех трех направлениях уже сделано. То, что сделанное действительно представляет интерес, подтверждают
специалисты в области финслеровых пространств. Отрицательные же заявления звучат исключительно от не специалистов, основанные как правило на их математической и физической интуиции, заточенной под обычные квадратичные геометрии. Разве так можно?
Попробуйте набраться немного сомнения в собственной правоте и просто поработать с имеющимися четырехмерными объектами. В частности, рассмотрите поле, которое является четырехмерным аналогом поля двумерного точечного источника, то есть, задаваемое гиперкомплексным потенциалом на четверных числах
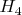
:

Надеюсь, даже без опыта работы с четырехмерными финслеровыми пространствами с метрикой Бервальда-Моора, легко понять, что это поле одиночного гиперболического точечного источника, являющегося естественным расширением двумерного гиперболического точечного источника на псевдоевклидовой плоскости. С ответом на вопрос: "На сколько такие объекты имеют аналоги в реальном четырехмерии?" - вполне можно повременить. Поразвлекаться, так сказать, с одними математическими и геометрическими конструкциями..
Следующее, что приходит на ум - это рассмотреть четырехмерные гиперболические вихри, которые при желании можно именовать гиперболическими четырехмерными монополями. Надеюсь, почти очевидно, что гиперкомплексные потенциалы соответствующих векторных полей должны иметь вид:



Что особенно интересно, обычные магнитные монополи, во всяком случае те, как их понимают некоторые физики, еще большой вопрос что существуют, тогда как описанные выше четырехмерные гиперболические вихревые монополи, по крайней мере в рамках конкретного математического финслерова пространства, точно имеются и могут очень даже подробно изучаться. Если в чем и можно сомневаться, так это в том, стоЯт ли за ними какие-то реальные физические объекты, но это вопрос уже к экспериментаторам.
Как и на комплексной плоскости, отталкиваясь лишь от одной элементарной аналитической функции логарифм можно построить
практически любую аналитическую функцию, которая будет являться либо суперпозицией множества логарифмов со своими обильностями (весовыми коэффициентами), либо производными, либо интегралами. По сути это напоминает разложение функции в ряд Лорана, только в данном случае, переменная не вещественная или комплексная, а гиперкомплексная. На уровне геометрического восприятия данного приема все сводится к четырехмерным пространственным комбинациям множества гиперболических источников и вихревых монополей, а так же множества мультиполей разного уровня. Распределения таких особенностей так же не обязаны быть дискретными множествами, как и на комплексной плоскости, можно рассматривать и непрерывные распределения мультиполей.
От четырехмерного пространства с финслеровой метрикой Бервальда-Моора достаточно естественно и относительно просто можно перейти к связанной с ней метрикой пространства Минковского. Как объясняли мне физики, соответствующая процедура носит название соприкосновения вдоль опорного векторного поля. После первого этапа проведения такой операции из метрики с четвертыми степенями компонент получается кубическая метрическая функция, а после применения дважды - квадратичная. Что интересно, если функция заданная на четверных числах аналитическая, в качестве автоматического следствия такой процедуры всегда получается четырехмерное плоское пространство-время Минковского, но если функция не аналитическая, то поучается уже собственно кривое псевдориманово пространство-время, метрика которого имеет сигнатуру (+,-,-,-). Пока не очень понятны физические основания к проведению такой процедуры, но сам факт и его последствия, на мой взгляд, говорят, что такие основания рано или поздно найдутся. Если, конечно, их искать, а не говорить как Вы, мол, нет никакой мотивации..
Цитата:
Не вижу, как может быть убедительным аргумент с переносом некоторого класса (элементарных функций) решений уравнения Лапласа на формульном уровне в решения волнового уравнения.
Надеюсь Вы знакомы с фактом, что если конструировать некое поле на комплексной плоскости произвольным образом размещая на ней источники, стоки, вихри, мультиполи, на формульном уровне воплощающееся в переходе от элементарных функций к произвольным аналитическим, получающееся в итоге поле является в обязательном порядке решением двумерного уравнения Лапласа. Аналогичным образом обстоят дела и на плоскости двойной переменной с той разницей, что уравнение Лапласа тут заменяется двумерным уравнением Даламбера. При этом не обязательно ограничиваться одними конформными преобразованиями, можно захватить и квазиконформные. В этом случае возникает связь уже не с уравнениями двумерного Лапласа или Даламбера, а с уравнениями Пуассона, кажется. Почти так же обстоят дела и в случае с четырехмерным пространством четверных чисел. Только фундаментальное уравнение тут не второго порядка, как Лапласа и Даламбера, а четвертого. Его вид тесно связан с метрикой вида (1), выписанной ранее. Его решениями всегда и оказываются те поля, которые конструируются из конечного или бесконечного множества четырехмерных гиперболических источников и гиперболических вихрей. И тут так же в параллели с таким контруированием возникают аналитические функции, существенно более сложные чем просто элементарные. Их множество бесконечномерно. Но и это еще не предел. Принципиально нет особых сложностей перейти от аналитических функций к более сложно устроенным. Для связанных с ними преобразований инвариантом оказываются уже не углы, а полиуглы, которых не было в квадратичных геометриях. Такие функции при переходе от метрики четвертого порядка к квадратичной, порождают как я писал выше уже кривые псевдоримановы пространства. В частности, можно задаться вопросом, как должна выглядеть неаналитическая функция от четверных чисел, что бы в соприкасающемся псевдоримановом пространстве появлялись метрики Фридмана, Шварцшильда, Кэрра и Ньюмена.. Именно этот момент я имел ввиду, когда говорил о точных решениях уравнений Эйнштейна и их связи с двумерными задачами. С атомом водорода, полагаю, ситуация несколько иная, но "рыть" думаю нужно именно в этом направлении. Да и вообще квантовая механика при естественном использовании возможностей финслерова пространства четверных чисел могла бы существенно видоизмениться и во многом упроститься. Но ведь для этого нужно, что бы кто-то этим занялся, а у нашей маленькой группы на все это не хватает ни времени, ни сил, ни средств. У других же, как Вы говорите, не хватает мотивации..
Цитата:
Теоретическая физика --- это свойства уравнений, а не их конкретных решений. Сначала нужно доказать наличие связи между уравнениями, а потом заниматься переносом решений. Но на описываемом уровне свойства уравнений очень разные. Это тоже обсуждалось --- например, свойство однозначного продолжения решений.
Двойные и четверные числа это многомерные расширения алгебры действительных чисел. Со всеми из этого вытекающими достоинствами и недостатками. Одно из них - алгебраическая не замкнутость. То есть, не все алгебраические уравнения в таких числах имеют корни. Что бы выйти на аналог основной теоремы алгебры и каждое алгебраическое уравнение имело конкретное число корней, необходимо поступить как и с действительными числами. То есть, перейти из вещественной в комплексную область. Думаю, желаемое Вами свойство единственности аналитического продолжения нужно требовать не от функций над

, а от их комплексных расширений

. Но ведь нельзя делать все сразу. И комплексные числа появились в математике только тогда, когда более менее разобрались со многими свойствами и возможностями действительных чисел.
Цитата:
Т. е. сначала нужен какой-то общий принцип переноса, а затем уже можно говорить, что переносы конкретных решений имеют физический смысл.
Если говорить о неком фундаментальном принципе для поиска уравнений, геометрий и объектов, при использовании которых можно надеяться получить физически интерпретируемые результаты, могу еще раз сказать словами С.Вайнберга: "Важны не вещи, а принципы симметрий". От себя хочу лишь немного конкретизировать данный принцип: под симметриями должны пониматься метрически выделенные преобразования пространств, обладающих максимальным их разнообразием. На сегодня, как самые богатые на непрерывные и дискретные симметрии, я знаю только четырехмерные финслеровы пространства связанные с поличислами (не только четверные, есть еще несколько). В связи с последним обстоятельством можно сформулировать данный принцип и несколько иначе, примерно так, как утыерждал Пифагор: "Все сущее - суть числа". Немного так же добавлю от себя. Числа, естественно, не рациональные, а коммутативно-ассоциативные гиперкомплексные, то есть, поличисла с четырьмя вещественными или комплексными измерениями. Причем последние заведомо более интересные.
Цитата:
И принцип должен быть построен не для элементарных функций, а для некоторого естественно описываемого класса решений. И я верю, что такого принципа быть не может, поскольку уравнения и поведение их решений очень различны.
А я верю, что такой принцип может быть сформулирован и даже привел примеры двух немного отличающихся вариантов. Только Ваша вера принципиально не может быть подтверждена, тогда как моя приводит к идее не только теоретической, но и экспериментальной проверки. Более того, кое что мы в этом направление уже сделали. Про замечание в ограниченности одними элементарными функциями уже сказал выше. Никто ими и не ограничивается, просто идти логичнее от простого к сложному, от частного к общему, а не наоборот, как бы этого не хотелось..
Снова получилось чрезмерно длинно, но я не знаю как о мало известном Вам предмете писать в трех строчках..