Проблемы с биекцией

[Иван_85]

Nemiroff в сообщении #556601 писал(а):

Э-э-э. Тяжело вам, наверное, проверять функции на монотонность.
Погуглите, как выводится производная тангенса.

Я знаю как выводится производная тангенса.

[LaTeXScience]

Иван_85 в сообщении #556556 писал(а):

Ну область значения функции $f$ равна $\left(2;+\infty\right)$. Каждая точка из этого интервала принадлежит этому интервалу. И что это дает?

Это как раз и означает, что

Иван_85 в сообщении #556526 писал(а):

для любого $y\in \left (2; +\infty \right )$ существует $x\in\left (-2;1\right )$ такой, что $f(x)=y$

[Nemiroff]

Иван_85 в сообщении #556602 писал(а):

Я знаю как выводится производная тангенса.

И? Вы не можете сделать вывод, что тангенс возрастает, там где вам нужно?

[Иван_85]

LaTeXScience, понимаете что из того, что функция имеет не пустую область значений еще не следует, что эта функций является сюръекцией?

[LaTeXScience]

Иван_85 в сообщении #556556 писал(а):

Это равносильное утверждение. Я как раз и спрашиваю как это доказать.

Упростите, используя тождество $\tg \alpha \pm \tg \beta = \frac{\sin (\alpha \pm \beta)}{\cos \alpha \cos \beta}$, выражение $\tg\left(\frac{x_1+2}{6}\pi\right)-\tg\left(\frac{x_2+2}{6}\pi\right)$.

-- 05.04.2012, 17:45 --

Иван_85 в сообщении #556607 писал(а):

LaTeXScience, понимаете что из того, что функция имеет не пустую область значений еще не следует, что эта функций является сюръекцией?

ru.wikipedia.org/wiki/Область_значений_функции

[Иван_85]

Nemiroff в сообщении #556604 писал(а):

И? Вы не можете сделать вывод, что тангенс возрастает, там где вам нужно?

Могу. Но я это делаю, уже зная то, что тангенс в нужных местах является биекцией. А сам факт биекции устанавливается где-то раньше.

-- Чт апр 05, 2012 15:48:14 --

LaTeXScience в сообщении #556612 писал(а):

ru.wikipedia.org/wiki/Область_значений_функции

Все правильно. Отображение "в" еще не означает, что это отображение является "на".

[LaTeXScience]

Из того, что функция $f:X\to Y$ имеет область значений равную $Y$ (т.е. $f(A)=Y$), следует, что $f$ сюръективна.

[Иван_85]

LaTeXScience в сообщении #556614 писал(а):

Из того, что функция $f:X\to Y$ имеет область значений равную $Y$ (т.е. $f(A)=Y$), следует, что $f$ сюръективна.

Согласен.

[Nemiroff]

Иван_85 в сообщении #556617 писал(а):

А тот случай, когда $f(X)=Y$ называется сюръекцией.

Вам LaTeXScience ровно это и написал.

Иван_85 в сообщении #556613 писал(а):

Могу. Но я это делаю, уже зная то, что тангенс в нужных местах является биекцией. А сам факт биекции устанавливается где-то раньше.

Я, честно, абсолютно вас не понимаю.

[Профессор Снэйп]

Иван_85 в сообщении #556526 писал(а):

Помогите пожалуйста разобраться.
Докажите, что множества $\left (-2;1\right )$ и $\left (2; +\infty \right )$ равномощны.
Геометрически биекция строится легко. Но у меня возник вопрос в другом способе решения.
Легко можно увидеть, что функция $f=2+\tg\left (\frac{x+2}{6}\pi\right ):\left (-2;1\right )\rightarrow \left (2; +\infty \right )$, по-видимому, является биекцией между исходными интервалами, но ведь это еще нужно доказать. Или я ошибаюсь и тут больше ничего не нужно доказывать?
1. Проверка на инъекцию. Как убедиться в том, что для любого $y\in \left (2; +\infty \right )$ существует $x\in\left (-2;1\right )$ такой, что $f(x)=y$?
2. Проверка на сюръекцию. Как убедиться в том, что для любых $x_1, x_2 \in \left (-2;1\right ) \left( x_1 \neq x_2 \Rightarrow f(x_1)\neq f(x_2)\right)$?
Меня интересует строгая формальная сторона вопроса.

Да вроде про тангенс всё очевидно из средней школы. А если совсем строго... выписываем определение тангенса и чувствуем, как начинают шевелиться волосы на голове!

Кстати, можно и без тангенса.

$$ f(x) = \frac{6}{x+2} $$

достаточно

[Иван_85]

Профессор Снэйп, вот почему Вы так уверены в том, что для любого $y\in\left(2;+\infty\right)$ существует $x\in\left(-2;1\right)$ такой, что $f(x)=y$?
$f(x)=2+\tg\left(\frac{x+2}{6}\pi\right)$.
Я вот, например, утверждаю, что существует такой $y\in\left(2;+\infty\right)$, что для любого $x\in\left(-2;1\right)$ $f(x)\neq y$.
Как Вы это опровергните?

[Профессор Снэйп]

Иван_85 в сообщении #556676 писал(а):

Как Вы это опровергните?

Нарисую график тангенса и ткну в него носом!

Или Вы чего хотите? Чтобы я доказывал непрерывность тангенса, потом вычислял $\lim_{x \to \pi/2 - 0} \tg x$, потом ссылался на теорему о том, что непрерывная функция принимает на отрезке все промежуточные значения?.. Тогда уж надо будет начать с определения тангенса. Что это, по Вашему, такое?

[Иван_85]

Профессор Снэйп в сообщении #556682 писал(а):

Нарисую график тангенса и ткну в него носом!

Или Вы чего хотите? Чтобы я доказывал непрерывность тангенса, потом вычислял $\lim_{x \to \pi/2 - 0} \tg x$, потом ссылался на теорему о том, что непрерывная функция принимает на отрезке все промежуточные значения?.. Тогда уж надо будет начать с определения тангенса. Что это, по Вашему, такое?

Понятно.

[Профессор Снэйп]

Иван_85 в сообщении #556689 писал(а):

Понятно.

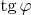
Чтобы стало ещё понятнее: $\tg \varphi$ - это величина $y/x$, где $(x,y)$ - точка на единичной окружности, такая что длина дуги окружности, заключённой между точками $(0,0)$ и $(x,y)$ равна $\varphi$. А что такое длина дуги? Уж не интеграл ли там какой-нибудь вырисовывается?.. И, главное, плохо не то, что интеграл, а то, что дуга параметризуется через синусы и косинусы, то есть мы теперь ещё и их должны определять!

Можно, конечно, пойти более простым путём и тупо положить $\tg x = \sin x / \cos x$. А затем взять по определению

$$ \sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \ldots; \,\,\,\,\, \cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \ldots $$

Затем показываем, что радиус сходимости обоих рядов бесконечен. Затем - ссылаемся на теорему о том, что аналитическая функция внутри круга с радиусом, равным радиусу сходимости ряда, дифференцируема. Затем вычисляем производные (тут, слаба Богу, можно сами ряды дифференцировать почленно, они друг в друга переходят), затем...

Короче, если хотите попроще, и при этом строго, то я Вам указал функцию без всяких тангенсов.