Что, прямо так очевидно? Во-первых, надеюсь, что группа все-таки конечна. Даже в этом предположении не факт, что можно обойтись без теоремы Машке.
-- 31.03.2012, 01:15 --И то не над всеми полями это работает. Или я туплю?
-- 31.03.2012, 01:18 --Например, википедия пишет, что это неверно в случае, если характеристика

делит
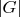
.
Если поле имеет конечную характеристику, а порядок (конечной) группы делится на эту характеристику, то групповая алгебра не полупроста и не является прямым произведением полей.
Если поле характеристики ноль, то групповая алгебра полупроста. Из этого следует, что она вкладывается в декартово произведение полей (группа коммутативна - это существенно), точнее, она является подпрямым произведением полей.