неизоморфность проколотого диска и кольца

[podsekalnikov]

Нужно доказать, что проколотый диск $D=\{\,z\mid 0<|z|<1\,\}$ неизоморфен кольцу $A=\{\,z\mid a<|z|<b\,\}$ $(0<a<b<\infty)$. Видимо здесь нужно как-то воспользоваться леммой Шварца, но что-то у меня не получается. Буду очень признателен вашей помощи.

[Padawan]

Пусть $f\colon D\to A$ -- конформное отображение. Функция $f$ ограничена в окрестности точки $z=0$. Поэтому она продолжается по непрерывности в эту точку, причем $f(0)\in \overline A$. Если в $D$ взять замкнутый круг радиуса меньше единицы с центром в нуле, то при помощи продолженного отображения $f$ можно будет организовать непрерывную ретракцию этого круга на свою границу. А это невозможно по теореме Брауэра.

[ewert]

Padawan в сообщении #548767 писал(а):

ретракцию этого круга на свою границу. А это невозможно по теореме Брауэра.

Мощно задвинуто. Где Брауэр -- а где ТФКП?... Что он Гекубе, что ему Гекуба?...

На самом деле всё сводится просто к тому, что аналитический образ области есть область. И, в частности, образ ноля для продолженной функции -- это внутренняя точка кольца. Поэтому в образ ноля должна переводиться некоторая внутренняя точка выколотого круга (раз уж ноль выколот). Но при этом явно нарушалась бы взаимная однозначность отображения (образ окрестности этой второй точки перекрывался бы с образом окрестности ноля), вот и всё.

А если вдруг захочется отказаться от изоморфизма и потребовать лишь аналитичность отображения, то и утверждение станет неверным.

[Padawan]

ewert в сообщении #549062 писал(а):

Padawan в сообщении #548767 писал(а):

ретракцию этого круга на свою границу. А это невозможно по теореме Брауэра.

На самом деле всё сводится просто к тому, что аналитический образ области есть область. И, в частности, образ ноля для продолженной функции -- это внутренняя точка кольца. Поэтому в образ ноля должна переводиться некоторая внутренняя точка выколотого круга (раз уж ноль выколот). Но при этом явно нарушалась бы взаимная однозначность отображения (образ окрестности этой второй точки перекрывался бы с образом окрестности ноля), вот и всё.

Согласен, так проще. Однако я на самом деле показал большее -- что при гомеоморфизме круга на кольцо в нуле отображение обязательно будет разрывным.

[ewert]

Padawan в сообщении #549078 писал(а):

Однако я на самом деле показал большее -- что при гомеоморфизме

Так ведь в ТФКП всё это вовсе не нужно. "Не следует плодить сущностей без необходимостей", как говаривал тов. Оккам.

[Padawan]

ewert в сообщении #549093 писал(а):

"Не следует плодить сущностей без необходимостей", как говаривал тов. Оккам.

Здесь это совершенно не к месту. Какую сущность я наплодил? Я же наоборот указал на более общий факт, чисто топологический.

[podsekalnikov]

Ваши рассуждения понятны, остался только один неясный момент: почему образ нуля для продолженной функции - это внутренняя точка кольца?

[ewert]

(Оффтоп)

Padawan в сообщении #549099 писал(а):

Я же наоборот указал на более общий факт, чисто топологический.

Так ведь он же (именно в силу общности) и гораздо более сложный. А к чему?... Ведь подавляющее большинство народонаселения, изучающего ТФКП, никакой топологии вовсе не изучают.

Вот это-то и есть Оккам.

-- Пт мар 16, 2012 23:07:49 --

podsekalnikov в сообщении #549105 писал(а):

почему образ нуля для продолженной функции - это внутренняя точка кольца?

Потому, что ноль -- внутренняя точка круга, а мы уже установили, что функция продолжается до аналитической во всём круге (т.е. вплоть до ноля), а аналитический образ открытого множества открыт.

На самом деле последнее утверждение есть очевидное следствие другого, более технического (которое потом в моей выкладке используется ещё раз): что образ любой окрестности точки аналитичности содержит некоторую окрестность образа центра той исходной окрестности. Что достаточно очевидно следует из разложимости аналитической функции в степенной ряд.

[Padawan]

ewert в сообщении #549107 писал(а):

Вот это-то и есть Оккам.

Почитал, что про этот принцип пишут в википедии. В каком-то смысле правы Вы, а в каком-то я. С одной стороны я использую более сложные рассуждения, привлекаю теоремы Брауэра, когда можно без неё обойтись. С другой стороны Вы использует принцип сохранения области, когда можно без него обойтись.

[ewert]

Padawan в сообщении #549123 писал(а):

С другой стороны Вы использует принцип сохранения области, когда можно без него обойтись.

В ТФКП (а именно об ней и речь) без него никак не обойтись, тут он фундаментален. А вот общетопологические соображения -- факультативны.

[Oleg Zubelevich]

Принцип сохранения области основан на теореме Руше, а теорема Руше, в ее общей версии, носит топологический характер и справедлива в $\mathbb{R}^m$. Из нее кстати следует теорема Брауэра.
Так, что любые попытки изъять задачи ТФКП из общего круга идей этого сорта выглядят противоестественно.

[ewert]

Oleg Zubelevich в сообщении #549172 писал(а):

Принцип сохранения области основан на теореме Руше,

Ни разу, это гораздо более элементарно. Не говоря уж о том, что всевозможные многомерные обобщения не имеют никакого отношения к задачке.

[Oleg Zubelevich]

ewert в сообщении #549200 писал(а):

Ни разу, это гораздо более элементарно.

Шабат Введение в комплексный анализ том 1. А Вы как его доказываете более элементарно?

[ewert]

Oleg Zubelevich в сообщении #549233 писал(а):

А Вы как его доказываете более элементарно?

Это прямое следствие теоремы об обратной функции: если $f(z)=w_0+(z-z_0)^kg(z)=w$, то $h(z)=\sqrt[k]{w-w_0}$, где функция $h(z)=(z-z_0)\sqrt[k]{g(z)}$ -- аналитическая в окрестности $z_0$ (в достаточно малой окрестности эта функция может быть выбрана однозначной, т.к. там $g(z)$ мало отличается от $g(z_0)\neq0$). И поскольку $h'(z_0)\neq0$ -- по теореме об обратной функции уравнение $h(z)=\sqrt[k]{w-w_0}$ имеет единственное решение при всех достаточно малых $w-w_0$. 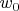А это ровно и означает, что достаточно малая окрестность образа $w_0$ содержится в образе некоторой окрестности точки $z_0$.

Правда, сам Шабат в вопросе об обратной функции проявляет некоторое легкомыслие. Сразу же после определения производной он говорит:

Цитата:

Поэтому в комплексный анализ без всяких изменений переносятся элементарные правила дифференцирования (дифференцирование суммы, произведения, частного, сложной и обратной функции); мы не останавливаемся на их формулировках и доказательствах.

Так вот: если доказательства первых четырёх свойств действительно переносятся один к одному, то с последним дело обстоит сложнее. Проблема в том, что эта теорема утверждает не только формулу для производной обратной функции (с которой всё действительно тривиально), но и существование обратной, и вот с существованием-то приходится повозиться. Во-первых, теорема об обратной функции требует (в отличие от предыдущих) не просто дифференцируемости, а непрерывной дифференцируемости, которой пока нет -- она появится гораздо позже, когда Шабат докажет теорему Коши и затем интегральные формулы Коши. Во-вторых (и в главных), теорема об обратной функции в комплексном варианте опирается (опять же в отличие от предыдущих) не на одномерную, а на двумерную аналогичную вещественную теорему. В-третьих, в комплексном варианте эта теорема обобщается (как было выше намёкнуто) с соответствующими оговорками на любые точки, а не только на те, в которых производная не равна нулю. То ли я не заметил, то ли Шабат теорему об обратной функции действительно нигде не обсуждает.

Ну как бы там ни было -- теорема эта всё-таки верна и гораздо принципиальнее и элементарнее, чем теорема Руше (для формального её доказательства достаточно в лоб применить принцип сжимающих отображений).

[Oleg Zubelevich]

ewert в сообщении #549293 писал(а):

То ли я не заметил, то ли Шабат теорему об обратной функции действительно нигде не обсуждает.

обсуждает сразу после теоремы о сохранении области. И доказывает теорему об обратной функции тоже из теоремы Руше. Я раньше туда просто не смотрел, доказывать теорему об обратной функции из теоремы Руше это не есть хорошо.