Дискретная математика и Кванты. Вентили

[loldop]

Здравствуйте!
Помогите разобраться с понятием "вентиля".
Цитата из учебника:
"Логические операции над двумя битами (Булевы функции) могут быть представлены символически на схемах. Каждая логическая операция представляется закрашиванием некоторой области на схеме. Докажите самым простым и наглядным способом то, что логических вентилей может быть ровно 16".

Вот, все понятно. Всего функций от двух переменных: $2^4 = 16$.
А что имеется ввиду под "вентилями". И как выглядит простейшая схема, допустим, ИЛИ в таком "закрашивании"?

[wallflower]

loldop в сообщении #550890 писал(а):

А что имеется ввиду под "вентилями"

Тот элемент схемы, который делает логическую операцию.

[loldop]

Хорошо, возможно ли доказательство через перебор всех вариантов?
А причем здесь "закрашивание области" на схеме?

[wallflower]

loldop в сообщении #550912 писал(а):

возможно ли доказательство через перебор всех вариантов?

Тогда вам нужно будет доказать, что вы перебрали все варианты.

Всё проще. У вас на входе ... возможных комбинации, на выходе ..., поэтому число возможных функций ...

[svv]

loldop писал(а):

И как выглядит простейшая схема, допустим, ИЛИ в таком "закрашивании"?

Вот здесь
http://en.wikipedia.org/wiki/Venn_diagram
видите пять бело-красных картинок с кругами? Это на кругах Венна изображены пять самых популярных функций из 16 возможных. Там есть и Ваше объединение (подпись Union of two sets: $A\cup B$).

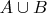
Два круга Венна делят всю схему на четыре области:
-- принадлежащая только левому кругу -- соответствует $x=1, y=0$
-- принадлежащая только правому кругу -- соответствует $x=0, y=1$
-- принадлежащая обоим кругам -- соответствует $x=1, y=1$
-- не принадлежащая ни одному из кругов -- соответствует $x=0, y=0$

Каждой функции двух переменных взаимно однозначно сопоставляется некоторый способ раскраски схемы -- каждая из четырех областей красится или не красится. Правило простое. Если для некоторой комбинации значений $x$ и $y$ функция должна выдавать $1$, соответствующая область закрашивается, а если должна выдавать $0$, то не закрашивается.

Легко понять, что при $4$ областях будет всего $2^4=16$ вариантов закраски. Я думаю, примерно это и имели в виду авторы книги.

[Евгений Машеров]

(Оффтоп)

А слово "вентиль" от того, что логические элементы "И" и "ИЛИ" выполнялись на диодах.