Задача с Белорусской республиканской олимпиады 11 класс

[MAnt]

Пусть $I$ - центр окружности, вписанной в остроугольный треугольник $ABC$, а $Q$ - точка касания вписанной окружности со стороной $AB$. На стороне $AB$ отмечена точка $T$, так, что $IT\parallel CQ $. Через точку $T$ проведена прямая, касающаяся вписанной окружности в точке $K$ (отличной от точки $Q$) и пересекающая прямые $CA$ и $CB$ в точках $L$ и $N$ соответственно.
Докажите,что $T$ - середина отрезка $LN$.

[Dave]

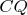
Пусть прямая $CQ$ пересекает окружность в точке $D$ (отличной от $Q$), а прямую $LN$ - в точке $E$. Поскольку $\angle IDQ=\angle IQD=\angle TIQ=\angle TIK$, то $\angle KID=\angle KIQ+\angle QID=180 \textdegree$, т.е. отрезок $KID$ - диаметр вписанной в $\triangle ABC$ окружности. Проведём через точку $D$ касательную к этой окружности, которая будет параллельна $LN$. Пусть эта касательная пересекает прямые $CL$ и $CN$ в точках $L'$ и $N'$ соответственно. Если мы применим к $\triangle LCN$ преобразование подобия с центром в точке $C$ и коэффициентом $\frac {CE} {CD}$, то $\triangle L'CN'$ перейдёт в $\triangle LCN$, а окружность, являвшаяся вневписанной в $\triangle L'CN'$ - в окружность, вневписанную в $\triangle LCN$ и касающуюся стороны $LN$ в точке $E$ (т.к. точка $D$ перейдёт в точку $E$). Пусть эта новая окружность касается прямой $CL$ в точке $F$, а прямой $CN$ - в точке $G$, а исходная окружность - в точках $H$ и $M$ соответственно.
Ввиду того, что $\triangle KIT \sim \triangle KDE$, $\frac {KT} {TE}=\frac {KI} {ID}=1$, т.е. $KT=TE$. Теперь применим свойство равенства касательных, проведённых из одной точки к одной и той же окружности:

$$LT-TN=(LK+KT)-(TE+EN)=LK+(KT-TE)-EN= LK-EN=LH-NG=$$

$$=(FH-LF)-(GM-NM)=((CF-CH)-LE)-((CG-CM)-NK)=(CF-CG)+$$

$$+(CM-CH)+(NK-LE)=0+0+(KT+TN)-(LT+TE)=TN-LT,$$

откуда следует, что $LT=TN$. $\blacksquare$

[Nikys]

Dave в сообщении #546007 писал(а):

Поскольку $\angle IDQ=\angle IQD=\angle TIQ=\angle TIK$

Можно ли спросить, как равенство последних двух углов к первым двум получается? Первых двух понятно ещё...

[Dave]

Nikys в сообщении #546130 писал(а):

Dave в сообщении #546007 писал(а):

Поскольку $\angle IDQ=\angle IQD=\angle TIQ=\angle TIK$

Можно ли спросить, как равенство последних двух углов к первым двум получается? Первых двух понятно ещё...

По условию $IT \parallel CQ$, значит $\angle TIQ=\angle IQC=\angle IQD$. У прямоугольных треугольников $KIT$ и $QIT$ одинаковые катеты $KI$ и $QI$ и общая гипотенуза, поэтому они равны и $\angle TIQ=\angle TIK$.

[Nikys]

Dave
Точно, туплю...

-- 07.03.2012, 22:51 --

Цитата:

$$LT-TN=(LK+KT)-(TE+EN)=LK+(KT-TE)-EN= LK-EN=LH-NG=$$

$$=(FH-LF)-(GM-NM)=((CF-CH)-LE)-((CG-CM)-NK)=(CF-CG)+$$

$$+(CM-CH)+(NK-LE)=0+0+(KT+TN)-(LT+TE)=TN-LT,$$

От рисунка, кстати, зависит, хоть и непринципиально. Просто по требованиям всеукраинских, к примеру, есть момент, что надо либо оптимизировать решение, показав все через один случай, либо рассмотрев разные случаи. Но думаю, тут это абсолютно непринципиально и пустяково.

[Dave]

Nikys в сообщении #546153 писал(а):

От рисунка, кстати, зависит, хоть и непринципиально.

Просто забыл сказать "не оганичивая общности, можно считать, что точка $T$ находится между точками $A$ и $Q$".