Понимание доказательства о гомоморфизме

[MagzhanZ]

Здравствуйте! У меня проблема с пониманием условия и доказательства теоремы о гомоморфизме.
Звучит примерно так:
1)$f: G \mapsto H $ - гомоморфизм групп.
2) $\pi: G \mapsto G/\operatorname{Ker} f$ -канонический гомоморфизм.
Тогда следует
1) Существует единственный гомоморфизм:
$\bar{f}: G/\operatorname{Ker} \to H$ и $\bar{f}\pi=f$
2) $G/\operatorname{Ker}f \cong \operatorname{Im}f$
3) Существует взаимно-однозначное соответствие между подгруппами $L$ группы $\operatorname{Im}f$ и подгруппами $M$ группы $G$, сохраняющее включение и нормальность подгрупп.
Теперь такой вопрос: как понимать предложение - сохраняющее включение и нормальность подгрупп.
Я в принципе не могу понять 3 пункт, его доказательство в том числе
Доказательство 3 пункта:
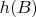
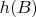
Любой подгруппе $B\in L$ cопоставим ее полный прообраз $h(B)$, а подгруппе $A\in M$ - подгруппу $f(A)$. Где $h(B)$ -обратная функция к $f$

(Оффтоп)

(не знаю, как написать f в минус первой)

[bot]

(Оффтоп)

MagzhanZ в сообщении #542765 писал(а):

не знаю, как написать f в минус первой

Очень просто - всё, что следует в фигурных скобках после значка ^, будет поднято над строкой, при отсутствии фигурных скобок будет поднят лишь один символ.

MagzhanZ в сообщении #542765 писал(а):

Теперь такой вопрос: как понимать предложение - сохраняющее включение и нормальность подгрупп

Это означает, что всякая (нормальная) подгруппа под действием отображения переходит в (нормальную) подгруппу - проверьте в порядке простого упражнения.

MagzhanZ в сообщении #542765 писал(а):

Любой подгруппе $B\in L$

Уже ерунда - это же памятник подгруппа, кто ж её заставит быть элементом?

[MagzhanZ]

bot в сообщении #542806 писал(а):

(Оффтоп)

MagzhanZ в сообщении #542765 писал(а):

не знаю, как написать f в минус первой

Очень просто - всё, что следует в фигурных скобках после значка ^, будет поднято над строкой, при отсутствии фигурных скобок будет поднят лишь один символ.

MagzhanZ в сообщении #542765 писал(а):

Теперь такой вопрос: как понимать предложение - сохраняющее включение и нормальность подгрупп

Это означает, что всякая (нормальная) подгруппа под действием отображения переходит в (нормальную) подгруппу - проверьте в порядке простого упражнения.

MagzhanZ в сообщении #542765 писал(а):

Любой подгруппе $B\in L$

Уже ерунда - это же памятник подгруппа, кто ж её заставит быть элементом?

Исправил-
Любой подгруппе $B\subset L$ cопоставим ее полный прообраз $f^{-1}(B)$, а подгруппе $A\subset M$ - подгруппу $f(A)$.

[bot]

Что за $M$? У нас есть гомоморфизм $f: G\rightarrow L=f(G)\subseteq H$. Вы берёте подгруппу $B$ в $L$ - хорошо. Покажите, что $f^{-1}(B)$ будет подгруппой в $G$. Пусть теперь дополнительно $B$ нормальна в $L$, покажите ...

[MagzhanZ]

bot в сообщении #542855 писал(а):

Что за $M$? У нас есть гомоморфизм $f: G\rightarrow L=f(G)\subseteq H$. Вы берёте подгруппу $B$ в $L$ - хорошо. Покажите, что $f^{-1}(B)$ будет подгруппой в $G$. Пусть теперь дополнительно $B$ нормальна в $L$, покажите ...

Там же ясно сказано подгруппа $M$ группы $G$

[bot]

Ну, ясно так ясно.