Кол-во перестановок n!/2

[Folo4ka]

Задача из комбинаторики + немного графов:
Задано 2 метода транспозиций (перестановок местами 2 элементов перестановки):
1) Прямой метод:
i элемент перестановки ставится в начало, а i+1 в конец
2) Обратный метод:
i элемент перестановки ставится в конец, а i+1 в начало

допустим для перестановки 123 (мощность 3) будут следующие варианты:
1) пр. метод: 123(исходный), 213, 231, 132, 312 ,321 - итого 6 перестановок
2) обр. метод: 123(исходный), 231, 312 - итого 3 перестановки

как видите используя один из 2 методов получается кол-во всех перестановок равно не n!, а n!/2
причем я расписал и построил граф так же для 1234 (мощность 4) и получилось следующее:
1) пр. метод: 12 перестановок (n!/2)
2) обр. метод: 24 перестановки (n!)

то есть нельзя сказать что именно какой-то метод дает n!/2 перестановок, возможно, я предполагаю, что если мощность четная, то половина всех возможных перестановок получается прямым методом, а если мощность нечетная, то половина перестановок получается обр методом (но, возможно, это не так). Так же кол-во входящих и исходящих ребер каждой вершины графа (перестановки) равно n-1, в сумме те и те (n-1)*2

Задание в следующем: почему одним из методов получается лишь половина n!/2 перестановок и какие именно перестановки (вершины графа) входят в перестановки этого метода (граф), а какие не входят?

[Null]

Почитайте о четных перестновках.

[Folo4ka]

я читал и думал что, возможно, это путь к разгадке.
Перестановка четная, если содержит четное кол-во инверсий.

Но застопорился на понятии инверсия и, так и не могу понять, как посчитать их кол-во.

Даже если и разобраться... все сойдется к тому, что неполный граф перестановок будет состоять ТОЛЬКО из четных или нечетных перестановок? В этом и заключается причина, что графы полученные одним из способов неполные?

[ИСН]

"Только нечётных" не бывает. Бывает "только чётных" или "только всех". Да, дело в этом.

[Folo4ka]

спасибо за подсказку, разобрался как считать инверсии.
Тему можно закрыть.

[Folo4ka]

в этой теме возникли новые вопросы, вернее уточнения.

нужна формула для общего случая (n элементов) которая бы и являлась бы точным условием. причем с ней как-то должно быть связано кол-во инверсий слева и справа (что это такое вообще? какая инверсия называется слева, а какая справа? в инете не нашел инфы), а так же четность или нечетность мощности перестановки (или сама мощность). Ну и для обоих способов.

вот тут у меня полный ступор... ну помогло бы хотя бы понимание инверсии слева и справа

еще есть какие-то "красивые задачи" на графы что-ли... но в нете тож не смог их найти, если кто знает такую - дайте, они тоже как-то связаны с этим заданием

Случайно не эта теорема является ответом?

Цитата:

Теорема. Четные подстановки $A_n$ являются группой (подгруппой в группе подстановок $S_n$ ) $|A_n|=\frac{n!}{2}$ при $n \geq 2$.

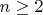
Доказательство. Так как произведение $\sigma\tau$ четных подстановок $\sigma$,$\tau\in A_n$ является четной подстановкой, то имеем операцию произведения на множестве $A_n$, которая ассоциативна. Тождественная подстановка четная и является нейтральным элементом в $A_n$. Если $\sigma\in A_n$, то мы уже отметили, что $\sigma^{-1}\in A_n$.