Задачи на интерференцию

[mirh]

Спасибо. Мне все понятно

-- Ср фев 08, 2012 13:15:48 --

Еще вопрос: написано, что при отражении от оптически более плотной среды происходит потеря полуволны. При этом в выражении для оптической длины пути следует добавить (или вычесть) слагаемое $\frac \lambda 2$. В каком случае надо добавлять, а в каком вычитать?

[Munin]

А какая разница между "добавить" и "вычесть" для $\lambda/2$?

[mirh]

$\frac \lambda 2$-это дополнительный путь света, который эквивалентен сдвигу по фазе на $\pi$. Получается нет разницы в какую сторону сдвигать?

[Munin]

Подумайте, есть ли разница между сдвигом по фазе на $\varphi$ или на $\varphi\pm 2\pi.$ Потом подставьте $\varphi=\pi.$

[mirh]

Нет разницы

[mirh]

Получается, при нахождении оптической разности хода нет разницы между $+\frac \lambda 2$ и $-\frac \lambda 2$?

[Munin]

Да! Вы же сами это получили, вы всё ещё не уверены?

[mirh]

Вот пример задания:
На стеклянную пластинку толщины $d_1$ и показателя преломления $n_1$ налит тонкий слой жидкости толщиной $d_2$ и показателем преломления $n_2$ ($n_1 < n_2$). На жидкость нормально падает свет с длиной волны $\lambda$. Оптическая разность хода интерферирующих волн равна:
1. $2d_2n_2$
2. $2d_2n_2 +\frac \lambda 2$
3. $2d_2n_2 -\frac \lambda 2$
4. $2d_1n_1$
Значит в этом задании и 2 и 3 правильные ответы?

-- Чт фев 09, 2012 15:34:15 --

И еще в учебнике Трофимова Курс физики в параграфе Интерференция света в тонких пленках написано:
Оптическая разность хода, возникающая между двумя интерферирующими лучами
$\delta=n(OC+CB)-(OA\pm \frac \lambda 2)$
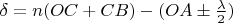
Если $n>n_0$, то потеря полуволны произойдет в точке $O$ и вышеупомянутый член будет иметь знак минус, если же $ n<n_0$, то потеря полуволны произойдет в точке $C$ и $\frac \lambda 2 $ будет иметь знак плюс ($n$-показатель преломления пленки, $n_0$- окружающей среды). Почему так?

[mirh]

Пожалуйста, помогите мне разобраться

[Munin]

mirh в сообщении #536678 писал(а):

Значит в этом задании и 2 и 3 правильные ответы?

А может быть, ни один из них?

[mirh]

Луч отражается от поверхности жидкости и преломляется. На границе воздух-жидкость происходит потеря полуволны. Преломленный луч доходит до границы жидкости и стекла, здесь тоже происходит отражение и преломление, т.е. луч проходит расстояние $2d_2$. Получаем, оптическая разность хода между отраженным лучом и преломленным равна $\delta=2d_2n_2 \pm\frac \lambda 2$. Разве не так?

[BISHA]

mirh в сообщении #536678 писал(а):

Почему так?

Жаль, нет рисунка.
В первом случае отражается от оптически более плотной среды луч сразу с поверхности, а в другом луч с внутренней поверхности. Я представляю это (для себя) так: при смене "направления движения" (отражение от оптически более плотной среды) фотон "тормозится" (часть его выходит за границу раздела - показывают опыты), его скорость уменьшается, что меняет фазу, но отражаясь летит дальше с той же скоростью. Если это происходит с лучем не проходящим во вторую среду, то нужно половину длины волны вычитать (торможение помогает уменьшить разность хода второму лучу. Но, если оптически более плотная среда окружает пластинку с меньшим показателем преломления, то "торможение" добавляет задержку и нужно прибавить половину длины волны. Здесь первый луч отражается от оптически менее плотной среды.

mirh в сообщении #536678 писал(а):

3. $2d_2n_2 -\frac \lambda 2$

Ваш ответ.

[mirh]

У меня есть методичка, там задача с решением: Определить результат интерференции световых лучей 1 и 2, отраженных от верхней и нижней поверхностей пластинки, в следующих случаях:
3) $n_1 < n > n_2$; 4) $n_1 > n < n_2$

Написано:
Результат интерференции зависит от оптической разности хода:
3) $\delta= 2dn + (\frac \lambda 2)$;
4) $ \delta= 2dn + (\frac \lambda 2)$.
Здесь ошибка?

[BISHA]

mirh в сообщении #537199 писал(а):

Результат интерференции зависит от оптической разности хода

Третий случай - $-\frac{\lambda}{2}$,
в четвертом - "+". Кажется так.

[mirh]

Спасибо, с этим я разобрался.
Есть задача:На поверхность тонкой прозрачной пленки ($n=$1,2) падает под углом $45^{\circ}$ свет с $\lambda=$550 нм. При какой наименьшей толщине пленки $d$ отраженный свет будет максимально ослаблен?
Я решал так: оптическая разность хода $\delta=2d\sqrt{n^2-{\sin^2 i}}+\frac \lambda 2$. Отраженный свет будет максимально ослаблен, если будет выполняться условие минимума:
$(2k+1)\frac \lambda 2=2d\sqrt{n^2-{\sin^2 i}}+\frac \lambda 2$. Получил выражение для $d$:
$d=\frac {k\lambda}{2\sqrt{n^2-{\sin^2 i}}}$.
Подставил $k=1$ и вычислил значение $d$. С ответом не совпадает. Что я делаю неправильно?