Добрый день.
Известно, что функция

принимает натуральные значения и для любых


или

. Также известно, что

. Найти

.
Единственное, что удалось понять, это
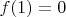
и

( использовал оценку снизу и то, что

или

). Очень смущает неопределенность для

.
Подскажите, пожалуйста, идею решения подобных задач.