Разве это условие не означает

?
Без аксиомы выбора - не означает.
Без аксиомы выбора мы можем построить сколь угодно длинную последовательность попарно различных элементов бесконечного (в смысле первого определения) множества

по такой схеме:
так как

, существует элемент

;
так как

, существует элемент

;
так как

, существует элемент

;
...
Повторив это рассуждение

раз, получим подмножество из

элементов

.
Однако бесконечную последовательность так получить нельзя, потому что для этого потребовалось бы бесконечно длинное рассуждение, а такие в математике не допускаются (вроде бы, есть какие-то бесконечные логики, допускающие бесконечно длинные формулы, но я о них ничего не знаю и об их применениях ничего не слышал; в любом случае, теория множеств с бесконечной логикой вместо классической - это не ZF).
Если же на множестве

есть функция выбора

(не важно, откуда она взялась, из аксиомы выбора или ещё откуда; например, если

- натуральный ряд, то для непустого подмножества

можно взять

), то мы можем формализовать предыдущее рассуждение как определение по индукции (аксиомы индукции доказуемы в ZF):
1) полагаем

,
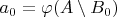
;
2) при

полагаем

,

.
Тогда

будет счётным подмножеством множества

.
Для множества

, бесконечного по Дедекинду, счётное подмножество можно построить таким образом. Пусть

- взаимно однозначное отображение на собственное подмножество. Определяем по индукции:
1)

; так как

, существует элемент

;

;
2) при

полагаем

,

,

.
Так как

взаимно однозначно, то при

выполняются условия

и

. Поэтому

при

, и

- искомое счётное подмножество множества

.
Если множество

содержит счётное подмножество

, то обозначим
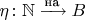
взаимно однозначное отображение натурального ряда на

. Тогда можно определить взаимно однозначное отображение

на собственное подмножество

следующим образом:

Поэтому множество

бесконечно по Дедекинду.