Так как

, Вы по значению тангенса можете восстановить угол

только до целого числа полуоборотов. При определении наклона прямых линий это не доставляет неудобств, так как прямая не изменится, если повернуть её вокруг какой-то её точки на

. Например, какой угол наклона имеет прямая

к оси абсцисс:
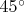
или

? Без дополнительных ограничений на угол оба ответа верны.
Другое дело, если у Вас не прямая, а луч или отрезок. Он уже не перейдет в себя, если его повернуть вокруг начала на

. В этом случае надо учитывать и синус, и косинус для правильного выбора угла.
Если же заниматься этим не хочется, то вот Вам формула, которая даст Вам угол по координатам

точки A без всей этой мороки. Я вывел её специально для Вас, и Вы первый, кто её видит:

Она
почти всегда срабатывает безотказно. Например, в Вашем случае имеем:




