Дираковские обозначения, простая задача.

[Himfizik]

nobody47 в сообщении #523175 писал(а):

3) готов согласиться с таким равенством:$<n|A|\psi>^{\dagger}=<\psi|A|n>$

Именно об этом исправлении Вам и говорили:

Himfizik в сообщении #522950 писал(а):

В одной из формул выше Вы потеряли сопряжение.

type2b в сообщении #523048 писал(а):

утверждение, что $<n|A|\psi>=<\psi|A|n>$ для эрмитова $A$ --- неверно

.

[type2b]

Himfizik в сообщении #523196 писал(а):

Именно об этом исправлении Вам и говорили

так точно.



А зачем там болтается единичный оператор, если не секрет?

И еще: полезно понимать, что это все есть ничто иное как линейная алгебра. Функции и интегралы -- просто представление, но все формулы верны в абстрактном случае. Скажем, если у вас не частица в ящике, а спин, то интегралов не будет, а утверждение про $A^2$ останется.
Кстати, контрольный вопрос: что такое $\psi(x)$ на языке линейной алгебры?

[nobody47]

type2b в сообщении #523225 писал(а):

[quote="Himfizik в [url=http://dxdy.ru/
Кстати, контрольный вопрос: что такое $\psi(x)$ на языке линейной алгебры?

Вектор.

Единичный оператор там остался из навязчивой идеи его использовать. Но решение предложенное вами я понял, большое спасибо:D

[type2b]

да, можно рассматривать $\psi(x)$ как элемент линейного пространства. А если мы работаем в дираковских обозначениях, т.е. $|\psi\rangle$, $|n\rangle$ и т.п., то чему равна функция $\psi(x)$?
Т.е. как устроен изоморфизм между абстрактным линейным пространством состояний и линейным пространством функций от икс?

[nobody47]

Пусть система описывается функцией $\psi$. Измеряемые физ. величины в нашей квантовой системе могут принимать дискретные значения (собственные), $a_i$. Тогда $\psi=\sum\psi_i$, каждая $\psi_i$ описывает состояние, где измеряемая величина может принимать лишь одно значение, с некоторой вероятностью.
Вот вроде так.

[type2b]

не просто величины, а полный набор коммутирующих наблюдаемых, но я не про это.
Подсказка, почти ответ: в гильбертовом пространстве можно рассмотреть состояния, являющиеся собственными для какого-нибудь оператора. Например, $|p\rangle$ -- состояние с определенным импульсом, $|x\rangle$ -- состояние с определенной координатой. Пусть $|\psi\rangle$ -- просто какое-то состояние. Чему для него равна волновая функция в координатном представлении (выразить через уже известные величины :)))

[nobody47]

$\psi(x,t)=\langle x|\psi(t) \rangle$
А я думал я понял азы уже)). А тут так в грязь лицом, спасибо что ткнули, а то потом посыпался бы..
П.С. координатное представление нагло стырено с вики:))) Пойду разбирать эту часть.

[type2b]

Да, правильно. Опять же, все это просто линейная алгебра, разные представления (координатное, импульсное, ...) -- разные базисы.

Пусть для начала гильбертово пространство конечномерно (или хотя бы имеет счетный базис). Выберем какой-нибудь базис $|n\rangle$. Это могут быть собственные векторы самосопряженного оператора, например. Если этот оператор $\hat{A}$ соответствует наблюдаемой $A$, то в состоянии $|n\rangle$ наблюдаемая будет принимать значение $a_n$, $\hat{A}|n\rangle=a_n |n\rangle$. Теперь рассмотрим произвольное состояние $|\psi\rangle$, разложим по нашему базису: $|\psi\rangle=\sum_n \psi(n) |n\rangle$, где $\psi(n)=\langle n|\psi\rangle$, если векторы $|n\rangle$ были отнормированы на единичную норму. Можно набор координат $\psi(n)$ рассматривать как функцию от $n$, это и есть волновая функция. Вероятность найти систему в состоянии $|n\rangle$ равна $|\psi(n)|^2$ (квардат проекции вектора состояния на $n$-е собственное состояние наблюдаемой $A$).
Можно сменить базис -- выбрать в качестве базисных векторов собственные векторы другого оператора, какого-нибудь $\hat{B}$. Тогда получим волновую функцию в $B$-представлении, это будет $\tilde{\psi}(m)$. Задача: найти, как $\tilde{\psi}(m)$ связана с $\psi(n)$ (в ответ будут входить собственные векторы $\hat{A}$ и $\hat{B}$. (Собственно, это просто изменение координат при смене базиса).

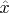
Теперь можно рассмотреть непрерывный спектр. В качестве оператора $\hat{A}$ выберем оператор координаты $\hat{x}$. Его собственные векторы маркируются непрерывным параметром $x$ (это вместо $n$ стало): $\hat{x}|x\rangle=x |x\rangle$. Раскладываем по ним, получаем волновую функцию в координатном представлении. Задача:
1. найти волновую функцию состояний $|x\rangle$ в координатном представлении, сравнить с "волновой функцией" собственных состояний $\hat{A}$ из предыдущего параграфа в $A$-представлении.
2. вместо оператора $\hat{B}$ взять оператор импульса. Используя результаты предыдущего параграфа, найти преобразование волновых функций из координатного в импульсное представление. Найти волновые функции собственных состояний оператора $\hat{p}$ в импульсном и координатном представлении.

Небольшая тонкость: для непрерывного спектра нормировка отличается от нормировки дискретного спектра. Вообще, с нормировками нужно еще отдельно поиграть.

Если вы эти элементарные упражнения проделаете, то вы будете понимать дираковскую формулировку QM.

[ChaosProcess]

А вот у меня тоже есть вопрос: как формально совершается переход от счетного базиса к несчетному для скалярного произведения? Все таки в первом случае у нас ряд в качестве скалярного произведения, а во втором интеграл.

[Ilia_]

ChaosProcess в сообщении #524915 писал(а):

А вот у меня тоже есть вопрос: как формально совершается переход от счетного базиса к несчетному для скалярного произведения? Все таки в первом случае у нас ряд в качестве скалярного произведения, а во втором интеграл.

Не просто интеграл, а интеграл Лебега. Он может браться и от дельта-функций. Отсюда сумма по дискретному спектру и получается.

[ewert]

Ilia_ в сообщении #524943 писал(а):

интеграл Лебега. Он может браться и от дельта-функций.

Нет, от дельта функций интеграл Лебега браться всё-таки не умеет. А сумма по дискретному спектру получается из-за совсем другого интеграла, которого зовут Стилтьесом.

[ChaosProcess]

Посмотрел определение Стилтьеса но не понял как его применять для дискретного спектра. ewert, можете расшифровать?

Ilia_ в сообщении #524943 писал(а):

Не просто интеграл, а интеграл Лебега. Он может браться и от дельта-функций

не, ну это наверно не так) Интеграл Лебега можно брать от измеримых функций. В случае дельта-функции(а точнее функционала) непонятно как выделять алгебру на пространстве основных функций.

[Ilia_]

(Оффтоп)

ewert в сообщении #524951 писал(а):

Ilia_ в сообщении #524943 писал(а):

интеграл Лебега. Он может браться и от дельта-функций.

Нет, от дельта функций интеграл Лебега браться всё-таки не умеет. А сумма по дискретному спектру получается из-за совсем другого интеграла, которого зовут Стилтьесом.

Да, действительно, перепутал... Про то, что из интеграла Стилтьеса получается сумма нам упоминали в курсе теории вероятности, но без чёткого определения. Вот и не отложилось в памяти толком. Mea culpa.

[nobody47]

Спасибо всем, кто помогал, в особенности type2b))
Тема дираковских обозначений для меня раскрыта)

[ewert]

ChaosProcess в сообщении #525326 писал(а):

Посмотрел определение Стилтьеса но не понял как его применять для дискретного спектра. ewert, можете расшифровать?

Могу. Любой самосопряжённый оператор представляется в виде интеграла Стилтьеса по своей спектральной мере: $A=\int\limits_{-\infty}^{\infty}\lambda\,dE(\lambda)$. Формально тут интеграл -- по всей оси, но фактически -- только по спектру оператора, т.е. по множеству тех точек, в которых функция $E(\lambda)$ (это -- операторнозначная функция числового аргумента, значениями которой являются спектральные проекторы) действительно изменяется. И если, например, спектр оператора чисто дискретен, то этот интеграл фактически превращается в ряд (или в конечную сумму): $A=\sum\limits_k\lambda_kP_k$, где $P_k$ -- это ортопроекторы на соотв. собственные подпространства. Если же спектр чисто непрерывен, то это действительно интеграл. Ну и возможны (причём реально возможны) комбинированные варианты.