AMapyaK, хорошее доказательство. Идея моего состоит в том, чтобы свести дело к случаю, когда рассматриваемое множество - компакт на прямой, а потом, методом бесконечного деления этого множества "пополам", доказать, что точек в нём "не меньше", чем в отрезке прямой. Подробно это выглядит так.
Пусть

- несчётное замкнутое множество в
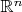
. Поскольку
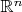
имеет мощность континуума (

), то мощность

не больше мощности континуума (

) и достаточно доказать, что она не меньше мощности континуума (

).
Рассматривая последовательность множеств

, где

- замкнутый шар с центром в начале координат и радиусом

, видим, что

, поэтому среди
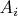
есть хотя бы одно несчётное множество. При этом соответствующее
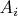
замкнуто и имеет мощность не большую, чем у

, и если мы докажем, что

, то тогда и

. Значит, не умаляя общности, можно считать, что множество

ограничено.
Далее, рассматривая проекции ограниченного множества

на оси координат,

, где

, заключаем, что, поскольку

, то среди

есть как минимум одно несчётное множество. При этом, опять же, соответствующее

замкнуто и имеет мощность не большую, чем у

, и если мы докажем, что

, то тогда и

. Значит, не умаляя общности, можно считать, что

- ограниченное замкнутое подмножество
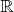
.
Лемма. Если множество ![$A \cap [p,q]$ $A \cap [p,q]$](https://dxdy-02.korotkov.co.uk/f/d/7/3/d7399e0376ffc8c61dbb1d5ee3d35ead82.png) несчётно, то существует такое число
несчётно, то существует такое число  ,
,  , что каждое из множеств
, что каждое из множеств ![$A \cap [p,r]$ $A \cap [p,r]$](https://dxdy-03.korotkov.co.uk/f/a/d/9/ad94eafaa48d2e48a45c72e75ea1514682.png) и
и ![$A \cap [r,q]$ $A \cap [r,q]$](https://dxdy-02.korotkov.co.uk/f/9/1/d/91d876b5421640a511fbd9458df9e6df82.png) несчётно. (Попросту говоря, каждый отрезок, содержащий несчётное число точек множества
несчётно. (Попросту говоря, каждый отрезок, содержащий несчётное число точек множества  , можно разбить на два отрезка, каждый из которых также содержит несчётное число точек множества
, можно разбить на два отрезка, каждый из которых также содержит несчётное число точек множества  .)
.)
Доказательство. Рассмотрим числа
![$r_-=\sup \; \{x \in [p,q] \, | \, card \; (A \cap [p,x]) \leq \aleph_0\}$ $r_-=\sup \; \{x \in [p,q] \, | \, card \; (A \cap [p,x]) \leq \aleph_0\}$](https://dxdy-02.korotkov.co.uk/f/5/1/8/518974947774d7de206c8e9aad37384a82.png)
и
![$r_+=\inf \; \{x \in [p,q] \, | \, card \; (A \cap [x,q]) \leq \aleph_0\}$ $r_+=\inf \; \{x \in [p,q] \, | \, card \; (A \cap [x,q]) \leq \aleph_0\}$](https://dxdy-01.korotkov.co.uk/f/4/1/b/41b81d34d091a9bd34dcf20a991448b482.png)
(

- мощность счётного множества). Эти определения корректны, т.к. множества, для которых берутся верхняя и нижняя грани, непусты. Первое из них содержит, как минимум, точку

, второе - точку

. Кроме этого, числа

и

принадлежат отрезку
![$[p,q]$ $[p,q]$](https://dxdy-03.korotkov.co.uk/f/6/f/0/6f0a8d0860a07f2998b96c110c0cdc2082.png)
. Из определений точной верхней и нижней граней следует, что можно выбрать последовательности

и

, такие, что

и

при любом

,

,

и
![$card \, (A \cap [p,x_m^-]) \leq \aleph_0$ $card \, (A \cap [p,x_m^-]) \leq \aleph_0$](https://dxdy-04.korotkov.co.uk/f/7/3/1/731e13dcb5ddb1d61e93df1e0079470382.png)
,
![$card \, (A \cap [x_m^+,q]) \leq \aleph_0$ $card \, (A \cap [x_m^+,q]) \leq \aleph_0$](https://dxdy-04.korotkov.co.uk/f/3/a/f/3aff7a52b6def010653fe1c5acdbb7a682.png)
при любом

. Поэтому
![$A \cap [p,r_-) \subseteq \bigcup\limits_{m=1}^{\infty} A \cap [p,x_m^-]$ $A \cap [p,r_-) \subseteq \bigcup\limits_{m=1}^{\infty} A \cap [p,x_m^-]$](https://dxdy-03.korotkov.co.uk/f/2/b/e/2be9222fa010891d6d9622d90a014d5782.png)
и

, аналогично
![$A \cap (r_+,q] \subseteq \bigcup\limits_{m=1}^{\infty} A \cap [x_m^+,q]$ $A \cap (r_+,q] \subseteq \bigcup\limits_{m=1}^{\infty} A \cap [x_m^+,q]$](https://dxdy-01.korotkov.co.uk/f/8/a/2/8a2a843ef9c2a296253380d0bcb2fe1982.png)
и
![$card \, (A \cap (r_+,q]) \leq \aleph_0$ $card \, (A \cap (r_+,q]) \leq \aleph_0$](https://dxdy-01.korotkov.co.uk/f/8/0/8/8081a0be62c4ee6e8e13f5a9d2c92f0782.png)
. Это говорит о том, что случай

невозможен, ибо тогда
![$[p,q] = [p,r_-) \cup \{r_-\} \cup (r_+,q]$ $[p,q] = [p,r_-) \cup \{r_-\} \cup (r_+,q]$](https://dxdy-03.korotkov.co.uk/f/e/1/e/e1ef8dd074570feb63d2df1a1768977d82.png)
и множество
![$A \cap [p,q] = (A \cap [p,r_-)) \cup (A \cap \{r_-\}) \cup (A \cap (r_+,q])$ $A \cap [p,q] = (A \cap [p,r_-)) \cup (A \cap \{r_-\}) \cup (A \cap (r_+,q])$](https://dxdy-02.korotkov.co.uk/f/1/d/2/1d2270cf8503c3640b1da02c1527d96082.png)
не более чем счётно, что противоречит условию леммы. В случае же

можно взять

. Тогда если бы, к примеру, множество
![$A \cap [p,r]$ $A \cap [p,r]$](https://dxdy-03.korotkov.co.uk/f/a/d/9/ad94eafaa48d2e48a45c72e75ea1514682.png)
было не более чем счётным, то верхняя грань

должна была быть не меньше

, что не так.
Построим функцию

, где

- множество конечных двоичных дробей на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
, следующим образом. Вначале положим

,

. Далее, для каждого

, если
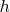
определена для дробей со знаменателями

и каждый отрезок
![$\left[h(\frac i {2^m}), h(\frac {i+1} {2^m})\right]$ $\left[h(\frac i {2^m}), h(\frac {i+1} {2^m})\right]$](https://dxdy-04.korotkov.co.uk/f/b/8/f/b8f6b1d11c7e3e846fc40d57d324875e82.png)
,

, содержит несчётное число элементов множества

, то, пользуясь леммой, выберем для каждого

число

, такое, что

и каждый из отрезков
![$\left[h(\frac i {2^m}),z_i^{(m)}\right]$ $\left[h(\frac i {2^m}),z_i^{(m)}\right]$](https://dxdy-03.korotkov.co.uk/f/6/7/1/671d385d103a2742a3051c588206df2082.png)
и
![$\left[z_i^{(m)},h(\frac {i+1} {2^m})\right]$ $\left[z_i^{(m)},h(\frac {i+1} {2^m})\right]$](https://dxdy-04.korotkov.co.uk/f/7/2/e/72ea560ae551d0da555ef45af6f085b882.png)
содержит несчётное число элементов множества

, и положим

(значение функции в середине отрезка между двумя исходными дробями) равным

. По построению функции
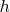
видно, что, если

, то

и на отрезке
![$[h(d_1),h(d_2)]$ $[h(d_1),h(d_2)]$](https://dxdy-04.korotkov.co.uk/f/7/3/a/73a610c74f4888b09d808bfd28c43c6b82.png)
содержится несчётное число точек множества

.
Наконец, построим функцию
![$f \colon [0,1] \to A$ $f \colon [0,1] \to A$](https://dxdy-04.korotkov.co.uk/f/3/5/6/356e2409f031cf3cc3c02d09f213536d82.png)
следующим образом. Для каждого числа

возьмём две последовательности конечных двоичных дробей

и

,

, сходящихся к

соответственно слева и справа и таких, что

и

при любом

. Для крайних точек отрезка,
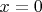
и

, будем брать соответственно

и

, оставляя то же требование для последовательности, сходящейся изнутри отрезка. Возьмём теперь любое число
![$x \in [0,1]$ $x \in [0,1]$](https://dxdy-01.korotkov.co.uk/f/c/9/f/c9f19ec3d2ee03aadf08a8f8bd185c8382.png)
. Каждый из отрезков
![$[h(d_m^-(x)),h(d_m^+(x))]$ $[h(d_m^-(x)),h(d_m^+(x))]$](https://dxdy-01.korotkov.co.uk/f/8/4/9/849b9fc316dda67ff986621c65dc689a82.png)
, очевидно, содержит несчётное число точек из

, поэтому мы можем выбрать в нём какую-нибудь точку

. Последовательность

ограничена, поэтому содержит сходящуюся к какому-то пределу подпоследовательность. В силу замкнутости множества

, этот предел также принадлежит

. Положим

равным этому пределу. Построенная таким образом функция

будет строго монотонной на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Действительно, если
![$x_1<x_2, \, x_1,x_2 \in [0,1]$ $x_1<x_2, \, x_1,x_2 \in [0,1]$](https://dxdy-01.korotkov.co.uk/f/4/f/8/4f8a4458766d4aa9a8ee998eb9e290a182.png)
, то мы можем выбрать две конечные двоичные дроби

и
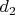
из

, такие, что

. При этом, начиная с некоторого номера

,

и

, следовательно, при всех этих

:

и

, откуда следует, что и для пределов частичных подпоследовательностей, выбранных при построении

и

, верно:

. Мы построили строго монотонное, а значит инъективное отображение

отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
, имеющего мощность континуума, во множество

, а значит мощность

не меньше

.




