(1) Рассмотрим функцию g(x)=

. Из условия следует, что функция g непрерывна и дифференцируема на

, g'(x)=2f'(x)(f''(x)+f(x)).
(2) Будем доказывать утверждение задачи от противного. Ввиду симметрии относительно замены x на x+t, можно считать, что g(0)=1+

, где

>0.
(3) Очевидно,

, а также

при всех

.
(4) Ввиду симметрии относительно замены x на -x, можно считать, что

.
(5) Покажем, что g'(x)>0 для всех неотрицательных

. Действительно, пусть для какого-то неотрицательного z выполняется g'(z)=0, а для всех неотрицательных y<z g'(y)>0. Тогда функция g(x) строго возрастает на [0, z) и g(z) > 1. По (1) g'(z)=2f'(z)(f''(z)+f(z))=0, откуда либо f'(z)=0, 1<g(z)=

, что противоречит условию, либо f''(z)=-f(z),

, 1<g(z)=

, что опять противоречит условию. Итак, при x>0 g'>0 (и, соответственно, g строго возрастает при x>0).
(6) Рассмотрим отрезок [0,

]. Если на всём этом отрезке

, то, интегрируя по этому отрезку функцию g, получим:

> 2, что противоречит (3). Значит, существует такое

>0, что g'(x)/2 = f'(x)(f''(x)+f(x)) <

.
(7) По (6) либо |f'(x)| <
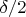
, либо |f''(x)+f(x)| <
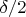
.
(8) В первом случае

<

, а по (5) (строгое возрастание) g(x) > 1+

, значит,

=g(x)-

> 1+

-

> 1, так как по (3)

<4. Получили противоречие с условием.
(9) Во втором случае, используя неравенство |f''(x)+f(x)|>|f(x)|-|f''(x)|, имеем: |f''(x)|>|f(x)| -
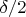
. Возводим в квадрат:

>

. Складывая это с неравенством

>

(следует из g(x) > 1+

), имеем:

>

. Опять противоречие с условием. Вуаля.
P.S. Однако, от души развлёкся с этой задачей. Подозреваю, что существует более красивое решение, но так его и не нашёл




